Dynamics of a Coupled Reactor-Separator System with Time Delay
Dynamics of a Coupled Reactor-Separator System with Time Delay
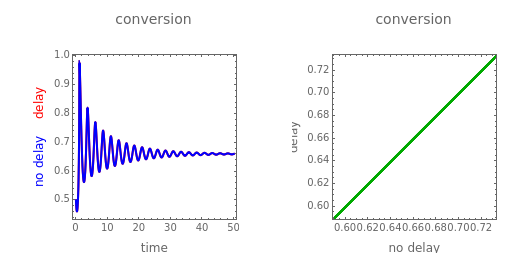
This Demonstration analyzes the effect of time delay on the behavior of a coupled non-isothermal continuous-flow stirred tank reactor (CSTR) with a separator.
The effluent of the reactor is fed to an isothermal separator and the liquid stream of the separator is recycled to the reactor. A first-order exothermic irreversible reaction takes place in the reactor and there is a time delay in the transport from the reactor to the separator. The dimensionless delay-differential equations that describe the system (equations 8 and 9 in [1]) are
A→B
τ
dz
dt
x
af
z(t-τ)-
y
e
x
e
y
e
x
e
x
af
D
a
T
e
dT
dt
1
γ
D
a
T
e
z(-τ≤t≤0)=
z
0
T(-τ≤t≤0)=
T
0
In these equations, represents the mole fraction of species in the reactor, is the reactor dimensionless temperature, and is the dimensionless time. , , and are the Damköhler number, the dimensionless heat transfer coefficient, and the dimensionless adiabatic temperature rise; these dimensionless numbers are defined in terms of system variables in the reference.
z
A
T
t
D
a
β
γ
The mole fractions of species in the reactor fresh feed, the distillate stream, and the recycle stream are , , . The equations are solved with and . In the absence of delay, the coupled system exhibits damped oscillations leading to a steady state for low and high values of the Damköhler number and oscillations without a steady state for intermediate values of the Damköhler number. Delay induces new regions of dynamic instability: increasing the delay beyond a lower threshold value can either destabilize the system or lead to isolated states of stability.
A
x
af
y
e
x
e
(β,γ)=(4.2,14)
(,,,,)=(0.45,0,0.9,0.8,0.2)
z
0
T
0
x
af
x
e
y
e