Descartes's Geometric Solution of a Quadratic Equation

a

25

b

8

z

1

= MR = 22.1047

z

2

= MQ = 2.89531

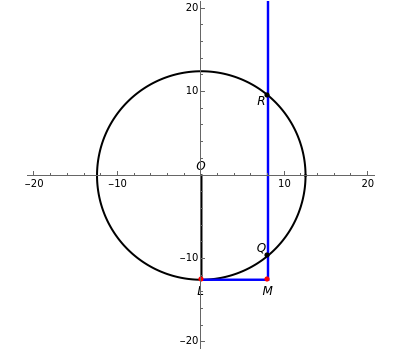
This Demonstration shows Descartes's geometric solution of the quadratic equation

2

z

=az-

2

b

in the unknown

z

. Consider a circle of radius

a/2

and let the points

M

and

L

be at

(b,-a/2)

and

(0,-a/2)

; the circle meets the negative

y

axis at

L

. Let the vertical line through

M

intersect the circle at

Q

and

R

. The solutions are then given by the intersections of the circle and the line. Thus the lengths

MQ

and

MR

are the two roots

z

1

and

z

2

of the original quadratic equation. When

b>

a

2

, the vertical line does not intersect the circle, meaning that the solutions to the quadratic are complex numbers. The

b

slider is therefore stopped at

b=

a

2

.

The well-known exact solutions to the above quadratic equation are

z=

1

2

a±

2

a

-4

2

b



.