WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

Cubic Equation of State for the Compressibility Factor

​
reduced pressure
1
reduced temperature
1
compressibility factors:
0.327226
In the Soave–Redlich–Kwong (SRK) equation of state (EOS), the compressibility factor occurs as a solution of the following cubic equation:
f(Z)=
3
Z
-
2
Z
+(A-B-
2
B
)Z-AB=0
,
where
A=
aP
2
(RT)
and
B=
bP
RT
with
a=0.42748α
2
(R
T
c
)
P
c
,
b=0.08664R
T
c
/
P
c
,
α=
2
1+m1-
T
re
, and
m=0.480+1.574ω-0.176
2
ω
. Here
ω
is the acentric factor,
T
c
and
P
c
are the critical temperature and pressure, and
T
re
=
T
T
c
is the reduced pressure.
When
T
r
and
P
r
=
P
P
c
are greater than one, the supercritical behavior is observed with
Z
varying continuously between low (close to zero, liquid-like behavior) and high values (near one, vapor-like behavior).
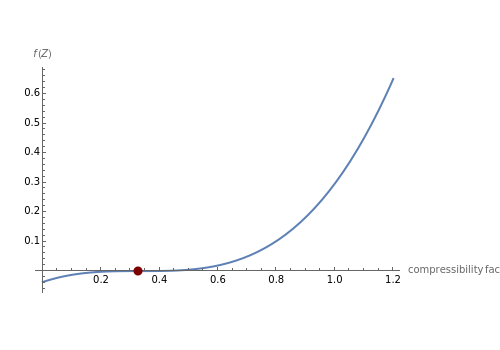
For specific values of
T
r
and
P
r
(when
P=
sat
P
, the saturation pressure, and
T<
T
c
), one gets three roots with the smallest and largest corresponding to the liquid and vapor phases. The intermediate value of
Z
has no physical significance.
The Demonstration plots
f(Z)
for ethane (
T
c
=305.43K
,
P
c
=48.84bar
, and
ω=0.09860
) and displays the location and values of its real roots.
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.