You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Cross Ratios in the Complex Plane
Cross Ratios in the Complex Plane
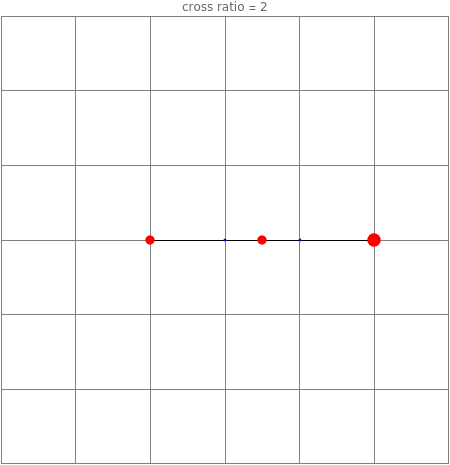
The cross ratio of four points , , , in the extended complex plane is defined by , where pairs of zeros or infinities that can be canceled should be. You can drag all four locators in the graphic.
z
1
z
2
z
3
z
4
λ=----
z
1
z
3
z
2
z
3
z
1
z
4
z
2
z
4
The cross ratio is the quotient of two ratios, -- and --. Suppose, for a moment, that the four points lie on a line. Then the ratio -- is a measure of the location of relative to and on the line, and similarly for --.
z
1
z
3
z
2
z
3
z
1
z
4
z
2
z
4
z
1
z
3
z
2
z
3
z
3
z
1
z
2
z
1
z
4
z
2
z
4
Projecting the four points on a line from a central eye point to another line distorts the relative distances of the new points , , , ; in general --≠-- and --≠--. However, the cross ratios remain equal: ----=----.
w
1
w
2
w
3
w
4
w
1
w
3
w
2
w
3
z
1
z
3
z
2
z
3
w
1
w
4
w
2
w
4
z
1
z
4
z
2
z
4
w
1
w
3
w
2
w
3
w
1
w
4
w
2
w
4
z
1
z
3
z
2
z
3
z
1
z
4
z
2
z
4
This is even true if the four points are not on a line, and the invariance holds more generally for any linear fractional transformation .
w=
az+b
bz+d
If the four points are unordered, there are six possible values (the red points; the cross ratio is bigger). They are shown as two triangles , , and , , , which are symmetric in the point . For orientation, and are drawn as small black points.
λ
λ
1/λ
1/(1-λ)
1-λ
1-1/λ
λ/(λ-1)
(1/2,0)
(0,0)
(1,0)
The cross ratio is real when the four points are on a circle or a line and is 2 for a square when the points are in cyclic order.