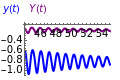
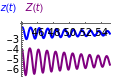
Coupled Lorenz Oscillators
Coupled Lorenz Oscillators
This Demonstration simulates the dynamics of two thermally coupled thermosiphons.
Thermosiphons are tubes filled with fluid that are bent into vertical closed loops that, when subjected to temperature differences, can convey heat due to buoyancy-driven flows; the tubes remove heat from the same source and exchange heat but do not exchange fluid. The equations describing the system are derived in the manner of the Lorenz system [1]:
dx
dt
dy
dt
Y
μ
1
P
dz
dt
dX
dt
dY
dt
1
P
dZ
dt
where , , and , , represent the temperature difference between descending and ascending fluids, the horizontal convective heat transport, and the azimuthal velocities of the two coupled thermosiphons. , , and are the Biot, Rayleigh, and Prandtl numbers and is the ratio of the vertical temperature gradients in the two tubes. If both loops are subject to the same external temperature, then and no heat is transported between the loops; when , the loops decouple and either loop can be used to represent the Lorenz system. In that case, for the second loop the equations are
x
y
z
X
Y
Z
B
R
P
μ=
Δ
T
1
Δ
T
2
μ==1
Δ
T
1
Δ
T
2
B=0
dX
dt
dY
dt
1
P
dZ
dt
These equations are the same as the Lorenz equations after a scale transformation and with the geometric factor set to unity; they have steady-state solutions and . More detailed explanation of the behavior of the equations used here can be found in [1] and [2].
(X,Y,Z)=(1,0,0)
{X,Y,Z)=,±,±
1
R
R-1
2
R
R-1