WOLFRAM|DEMONSTRATIONS PROJECT

Cooling by a Cylindrical Pin Fin

​
Biot number
1
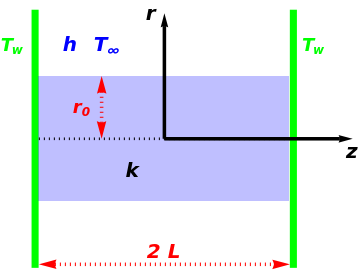
In electronic systems, a fin is a heat sink or a passive heat exchanger that cools a device by dissipating heat into the surrounding medium (e.g. air). This diagram shows a cylindrical pin fin, used to maximize heat transfer to a fluid between two walls:
The walls are at a high temperature
T
w
. The fluid flowing over the pin has a free stream temperature
T
∞
. The heat transfer coefficient between the pin wall and the surrounding medium is labeled
h
(in
W/
2
m
K
). If one introduces the dimensionless temperature
ϕ=
T-
T
∞
T
w
-
T
∞
, the governing equation is:
1
r
∂
∂r
r 
∂ϕ
∂r
+
2
∂
ϕ
∂
2
z
=0
,
with
0≤r≤
r
0
and
0≤z≤L
.
The associated boundary conditions are then:
∂ϕ
∂z
z=0
=0
(axial symmetry condition),
∂ϕ
∂r
r=0
=0
(radial symmetry condition),
∂ϕ
∂r
+
h
k
ϕ
r=
r
0
=0
(continuity of heat flux at the boundary fin/surrounding air), and
ϕ(z=L)=
ϕ
w
=1
(constant temperature at the wall),
where
k (W/m K)
is the thermal conductivity of the cylindrical pin fin and
r
0
=1
.
The Demonstration plots the contours of the dimensionless temperature for a user-set value of the Biot number. This solution is based on Chebyshev orthogonal collocation with
N=21
collocation points.
The analytical solution of the differential equation obtained by separation of variables [1] is given by:
ϕ=
∞
∑
n=1
2 
B
i
 
J
0
(
λ
n
 r)cosh(
λ
n
 z)
cosh(
λ
n
 L)
J
0
(
λ
n
r
0
)
2
(
λ
n
r
0
)
+
2
B
i

,where
B
i
=
h 
r
0
k
is the Biot number and
λ
n
are the zeros of the nonlinear function:
f(λ)=(λ 
r
0
)
J
1
(λ 
r
0
)-
J
0
(λ 
r
0
) 
B
i
.
We have found excellent agreement between our numerical solution and the analytical solution.