Convergence of Newton's Method for Approximating Square Roots
Convergence of Newton's Method for Approximating Square Roots
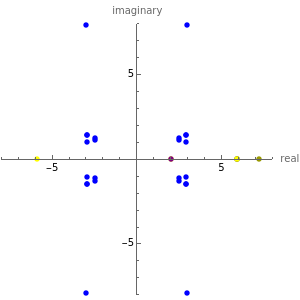
This Demonstration shows the convergence properties of a family of Newton-like methods for computing square roots of positive reals as constructed by Hernández and Romero. In this Demonstration the roots of 35 are used. For each integer , the iterative formula (displayed in the top left-hand corner) is defined. It generates a sequence (displayed below the formula) converging to one of the roots of 35 for almost all chosen starting values in the complex plane, outside the imaginary axis. The initial point is shown in purple, the two roots (limit points) are colored yellow, and some of the intermediate points are colored in shades of yellow, with darker colors corresponding to later positions in the sequence.
q≥2
Use the controls to vary the position of the starting point in the complex plane. Coloring each point in the plane according to whether the sequence with that initial point converges to the positive (pink) or negative (green) root yields an intricate fractal structure. A part of this structure can be seen by checking the fractal background checkbox. However, do not attempt to manipulate the controls with this option checked unless you are using a very fast computer.
The blue points belong to the so-called Julia set of the fractal. Close to these points convergence of the sequence becomes unpredictable.