Contours of Constant Principal Angle in the Complex Dielectric Plane
Contours of Constant Principal Angle in the Complex Dielectric Plane
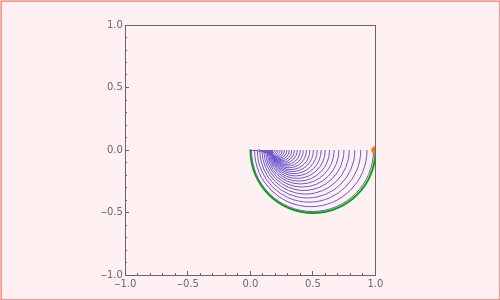
The contours of the constant principal angle in the complex dielectric plane can be determined by eliminating the principal azimuth from the equation . This gives , which is a circle with center at ϕ on the real axis and radius ϕϕ. The figure shows constant principal-angle contours for . As approaches , these contours approach concentric circles with center at .
ϕ
ϵ
ψ
ϵ=ϕ+ϕϕ
2
sin
2
sin
2
tan
-j4ψ
e
ϵ-ϕ=ϕϕ
2
sin
2
sin
2
tan
2
sin
2
sin
2
tan
0≤ϕ≤70°
ϕ
90°
ϵ=1