Continuous and Discrete Time Discounting

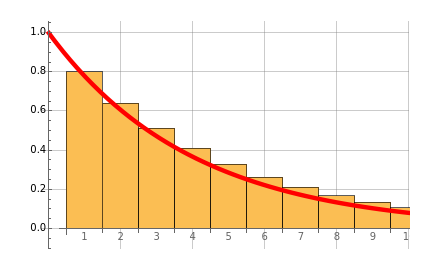
The well-known concept of discounting may be implemented as a discrete or continuous process in time, the first representing the common approach in financial institutions. The discrete time discounting term is

t

1

1+δ

, where

δ

is the discount rate and

t

is the time variable. The expression may be regarded as the present value of one unit of value at time

t

. For

δ>0

, the expression decreases over time. The corresponding continuous time expression is

-δt

e

. Note that

∞

∫

t=0

-δt

e

dt=

∞

∑

t=1

t

1

1+δ

=

1

δ

. The integral is shown as the PV (red) area (the present value of receiving one unit of value each unit of time eternally), while the PV (blue) area represents the sum. You can see the discrete time discounting as the light blue bars and/or a connecting blue line.