WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

Constructing a Regular Heptagon Using Lill's Method

​
radius
3
x
1.5
plot range
5
show labels
show x
show axes
show heptagon
show grid lines
fix first solution
fix second solution
fix third solution
P(x) =
3
x
+
2
x
-2x-1
P(x)
L
4
L'
3
x
1.625
1.625
1.5
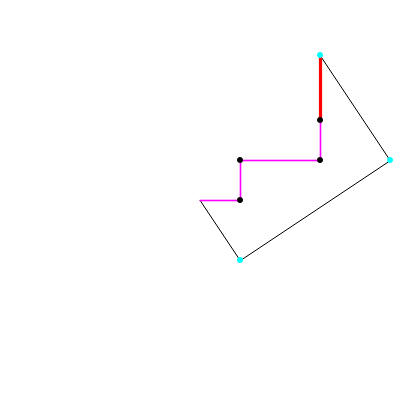
This Demonstration shows how to construct a regular heptagon using Lill's method for solving cubic equations.
The points of a regular heptagon with vertices on a circle of radius 1 are given by
7
z
=1
. Since
z=1
is a solution, if we divide the polynomial
7
z
-1
by
z-1
, we get
6
z
+
5
z
+
4
z
+
3
z
+
2
z
+z+1=0
.
If
z=cosϕ+isinϕ
, then
v=z+
1
z
=2cosϕ
.
Substituting
v=z+
1
z
leads to the cubic equation
3
v
+
2
v
-2v-1=0
.
It has solutions
2cos(2π/7)
,
2cos(4π/7)
,
2cos(6π/7)
.
This follows from the trigonometric identity
7
(2cosα)
-7
5
(2cosα)
+14
3
(2cosα)
-7(2cosα)-2cos7α=0
.
Set
7α=2π
and
x=2cosα
to get
7
x
-7
5
x
+14
3
x
-7x-2=0
,
which factors as
2
(
3
x
+
2
x
-2x-1)
(x-2)=0
.
There are solutions when the points
L
4
and
L'
3
coincide.
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.