Constructing a Regular Heptagon Using Gleason's Method
Constructing a Regular Heptagon Using Gleason's Method
This Demonstration shows Gleason's method for constructing a regular heptagon, using the following steps:
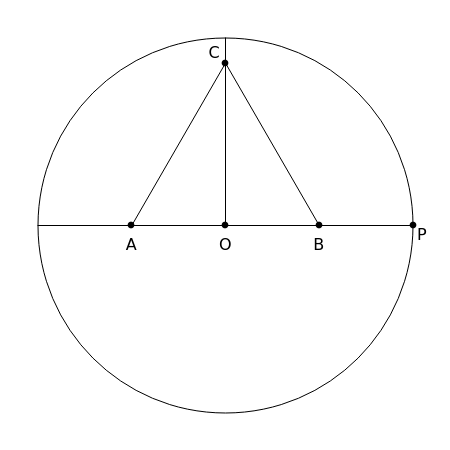
1. Draw a line segment of length 2 with midpoint and a circle with center and radius . Let , and be points on the line segment such that and . Draw an equilateral triangle .
O
O
1
A
B
P
AO=BO=1/2
OP=1
ABC
2. Draw a point between and so that . Draw an arc with center and radius . Let . The ray through with angle to meets the arc at a point .
D
A
O
DO=1/6
D
DC
3ϕ=∠CDB
D
ϕ
DP
F
3. The line perpendicular to through meets at and meets the circle at .
OP
F
OP
G
Q
4. The side length of the heptagon is and a compass can be used to measure out the other vertices of the heptagon.
PQ
Verification
tan(∠CDO)=3
3
cos(∠CDO)=cos(3ϕ)=
1
2
7
Therefore
4-3cosϕ=
3
(cosϕ)
1
2
7
Define
x
2
so that
cosϕ=+=
1
6
x
2
2
7
6
1+3x
2
7
Eliminating gives
ϕ
3
x
2
x
which has as its only positive solution (see Details).
x=2cos(2π/7)