Conjecture de Beraha pour les roues (French)

cycle d'ordre

B(1)	2cos 2π 1 +2	4	4.
B(2)	2cos 2π 2 +2	0	0.
B(3)	2cos 2π 3 +2	1	1.
B(4)	2cos 2π 4 +2	2	2.
B(5)	2cos 2π 5 +2	2+ 1 2  5 -1	2.61803
B(6)	2cos 2π 6 +2	3	3.
B(7)	2cos 2π 7 +2	2+2sin 3π 14 	3.24698
B(8)	2cos 2π 8 +2	2+ 2	3.41421

ShowreprésentationRacines[6,roue],représentationRacines[6,cycle],

,PlotRange{All,{-1.2,

1.1}},ImageSize{500,220},AspectRatio0.5,Background

,PlotLabel

Pour une roue construite à partir d'un cycle d'ordre 5,

les racines du polynôme chromatique de la roue : -1+(-2+x)

(-2+x)x sont montrées en vert,

les racines du polynôme chromatique du cycle : 1+(-1+x)

(-1+x) sont montrées en mauve,

et les nombes de Beraha sont montrés en rouge.



Le polynôme chromatique d'un graphe donne le nombre de façons de colorier le graphe avec

couleurs, sachant que deux sommets reliés ne peuvent pas avoir la même couleur.

Les nombres de Beraha sont

B(n)=2cos

2π

+2

Tutte a conjecturé qu'il y avait un lien entre les nombres de Beraha et certaines classes de graphes.

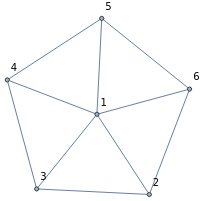
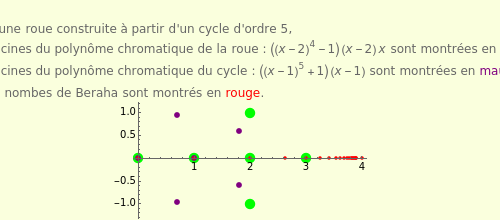
Cette Demonstration montre que pour un petit nombre de sommets il n'est pas évident de deviner le rapport qu'il y a entre les racines du polynôme chromatique d'un cycle (en mauve), celles de la roue correspondante (en vert) et les nombres de Beraha.

Alors que, avec un plus grand nombre de sommets, le lien est clair.