Complex Branching of Inverse Monomial Mappings from Lissajous Figures
Complex Branching of Inverse Monomial Mappings from Lissajous Figures
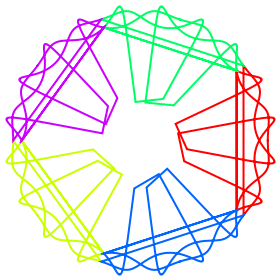
This Demonstration shows the branches of inverted monomial mappings from various Lissajous figures parametrized by . The symmetry is a direct consequence of the fundamental theorem of algebra: each point on the Lissajous figure maps via the inverse of to precisely radially symmetric points given by the roots of -=0. Since each branch preserves continuity, the Lissajous figure in its entirety is mapped to distinct radially symmetric branches. Each colored curve is the image of the Lissajous figure under a different branch of the inverse of .
(cos(mx),sin(nx))
z
0
p
z
p
p
z
z
0
p
p
z