Comparing Iterative Root-Finding Methods

number of iterations

5

function

sin(20x)-x

Oftadeh, Nikkhah-Bahrami, Najafi

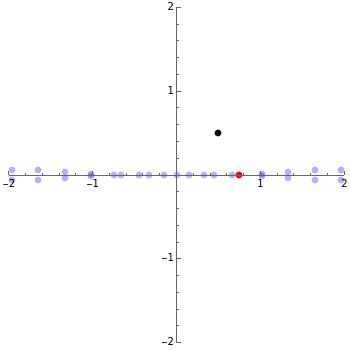
This Demonstration compares the effectiveness of a new iterative method of finding roots of nonlinear equations due to R. Oftadeh, M. Nikkhah–Bahrami, and A. Najafi and the classical Newton–Raphson method (implemented in Mathematica's FindRoot function). Choose a function

f

from the drop-down menu and the initial guess, which is a complex number

z

with

-2≤Re[z]≤2

,

-2≤Im[z]≤2

. The blue points show all the solutions of the equation

f=0

in this square (computed using Reduce). The red point shows the root found by the currently chosen method after the specified number of iterations. By increasing the number of iterations, a better approximation can be found. From these examples it can easily be seen that the new method is considerably more effective than the Newton–Raphson method, in general requiring many fewer iterations. Moreover, one can see some other interesting properties of the new method, like its ability to find complex roots starting with real initial values or starting from very distant initial values.