Classical Motion and Phase Space for a Harmonic Oscillator

initial conditions

~\)],

x

0

2

~\)],

p

0

-2

time

0

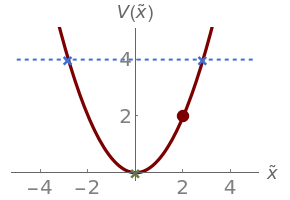
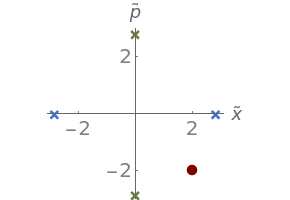
This Demonstration illustrates the classical harmonic motion of a particle governed by the Hamiltonian

H=

ω

2



2



p

+

2



x



, where the scaled variables are defined as



x

≡

mω

x

,



p

≡

p

mω

. Here



x

(t)

and



p

(t)

are obtained by solving Hamilton's equations of motion, subject to the initial conditions



x

0

=



x

(0)

and



p

0

=



p

(0)

. The three panels animate synchronously: (1) the motion of the particle in the potential; (2) the phase space trajectory; and (3) the time series of



x

(t)

and



p

(t)

. In the upper two panels, the points with minimum (turning points) and maximum momentum are labeled with blue and green

x

's, respectively.