Chemical Reactions Described by the Lorenz Equations

time

10.

x

0

32.

y

0

32.

z

0

32.

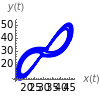
This Demonstration analyzes the behavior of a chemical reaction scheme that is described by the Lorenz equations:

dX

dt

=a(Y-X)

,

dY

dt

=bX-Y-XZ

,

dZ

dt

=XY-cZ

.

Parameters that lead to interesting behavior are

(a,b,c)=(10,28,8/3)

; the strange attractor that evolves from these equations spans both positive and negative values of

X

and

Y

. If we interpret these symbols as representing concentrations of chemical species, they cannot be negative; a shift of the

X

and

Y

axes can give new variables that are always positive [1]. Thus if we choose

x=X+δ

,

y=Y+δ

,

z=Z

with

δ=30

, the equations describing the system become

dx

dt

=-αx+αy

,

dy

dt

=bx-y+δz-xz-δ(b-1)

,

dz

dt

=-δx-δy-cz+xy+

2

δ

,where

x

,

y

, and

z

represent concentrations of chemical species. Using the values for the constants given above, the equations are

dx

dt

=-10x+10y

,

dy

dt

=28x-y+30z-xz-810

,

dz

dt

=-30x-30y-

8

3

z+xy+900

.

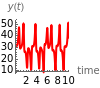
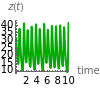
The reactions required to give the Lorenz equations are shown in section (1.7) of [1]. You can vary the time and the initial values of the species to see the evolution of the system. There is an unstable steady state at

(x,y,z)=(38.485,38.485,27)

and an unstable fixed point at

(x,y,z)=

72

+30,

72

+30,27

.