WOLFRAM|DEMONSTRATIONS PROJECT

Chaotic Attractor in Tumor Growth

length of simulation (time)

parameters

η

κ

ν

ω

ϕ

α

β

γ

δ

initial conditions

m(0)

f(0)

c(0)

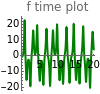
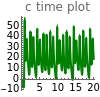
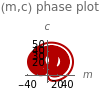
Model equations:

n'=0,f'=αη(m-f),m'=βκn-fc+γf-m,c'=νfm-ωn-δϕc

, where

n

,

m

,

f

and

c

are functions of time that represent tumor cell density, MDE (mucinous ductal ectasia) concentration, MM (malignant melanoma) concentration and oxygen concentration, respectively. These temporal equations were derived from a reaction-diffusion model from the tumor growth. The model mathematically describes both the processes of carcinogenesis and metastasis, as well as the sensitive dependence of cancer evolution on initial conditions and parameters. On the basis of this chaotic cancer attractor, a generic concept of carcinogenesis and metastasis is formulated.

Parameters:

α

= tumor cell volume (proliferation/non-proliferation fraction),

β

= glucose level,

γ

= number of tumor cells,

δ

= diffusion from surface (saturation level),

η

=

f

-decay (MM concentration),

κ

=

m

-growth (MDE concentration) and

ν

,

ω

,

ϕ

are

c

(oxygen concentration) growth and decay parameters.