Boole Differential Equation with Continued Fractions

n

γ

β

α

δ

k

xr

yr

Boole's Equation

γ

2

y(x)

+βy(x)+xα

′

y

(x)δ

k

x

-3x

′

y

(x)+3

2

y(x)

+4y(x)-2

5

x

-

2

3

5/2

x

J

-

11

15

2

5

2

3

5/2

x

J

4

15

2

5

2

3

5/2

x

-

4

3

-

2

5

x

-19-

6

5

x

-34-

6

5

x

-49-

6

5

x

-64-

6

5

x

-79-

6

5

x

-94+

6

5

x

109

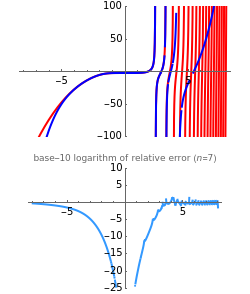
Explore the solutions of the Boole differential equation with continued fractions. Continued fractions provide a very effective function approximation toolset. Usually the continued fraction expansion of a given function approximates the function better than the Taylor series or the Fourier series. The solution(s) of the Boole differential equation are very diverse; they contain polynomials, trigonometric functions, hyperbolas, (nested) square roots, and modular forms.