Bohmian Quantum Trajectories for Coherent States of the Pöschl-Teller Potential
Bohmian Quantum Trajectories for Coherent States of the Pöschl-Teller Potential
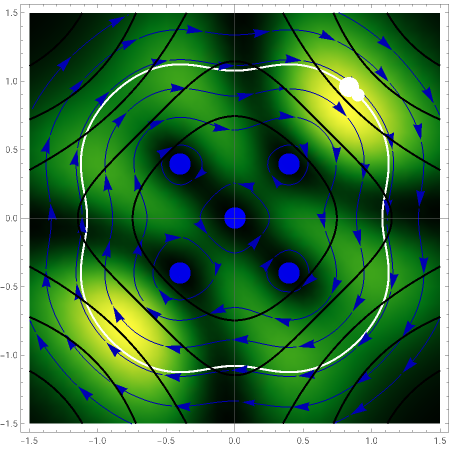
The trigonometric Pöschl–Teller potential (proposed for the first time in 1933 [1]) approximates the diatomic molecular potential energy. In the causal interpretation, superposed states, constant phase shifts, and non-factorizability are necessary for quantum motion to occur. Under certain circumstances, the motion might be chaotic (see Related Links). This Demonstration studies a two-dimensional version of the trigonometric Pöschl–Teller potential, which is in a special superposition state. If the perturbation term becomes zero (), the wave density (given by the square of the Schrödinger wavefunction) is not time dependent, but the corresponding autonomous differential equation system for the velocity field leads to a periodic motion in the configuration space. With the perturbation term, the Bohmian trajectory forms periodic, quasi-periodic, weak ergodic, or chaotic curves while interacting with the nodal points. Further investigations are necessary to capture the full dynamics of this system. The graphic shows the squared wavefunction, the trajectory (white), the nodal points (blue), the contour lines of the potential (gray), and the velocity field (red).
a=0