Bioeconomics of a Discrete Ricker Model with Delayed Recruitment

intrinsic growth rate (r)

fishing mortality (F)

entry

exit

cost/price ratio

time

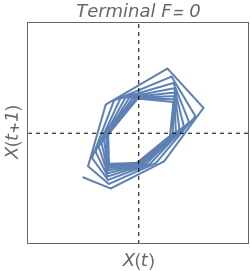
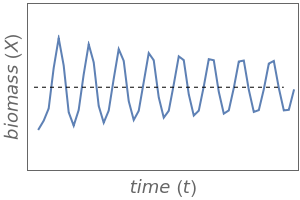
The discrete Ricker population model with delayed recruitment is given by

X

t+1

=

X

t

r1-

X

t-1



e

for a fish stock population.

X

t

denotes the stock biomass at time

t

and

r

is the intrinsic growth rate. An open access fishery is constrained by the biological properties of the stock, the cost/price ratio (cost of producing fishing mortality and unit price of harvest), and the rate of fleet entry/exit to the fishery. The entry/exit dynamics are linear to the profitability of the fishery, with increasing fishing mortality when economic rent (resource rent) is positive and decreasing fishing mortality when rent is negative. Stable equilibria are found as limit cycles or stationary equilibrium; chaotic behavior may also exist. While an increasing growth rate destabilizes the system, increasing fishing mortality tends to stabilize it. The natural equilibrium or stable focus (when fishing mortality is zero) is shown by the intersection of the two dashed lines. In the case of positive fishing mortality, corresponding equilibria are found south-west of the intersection between the dashed lines.