Binocular Disparity (Visual Depth Perception 7)
Binocular Disparity (Visual Depth Perception 7)
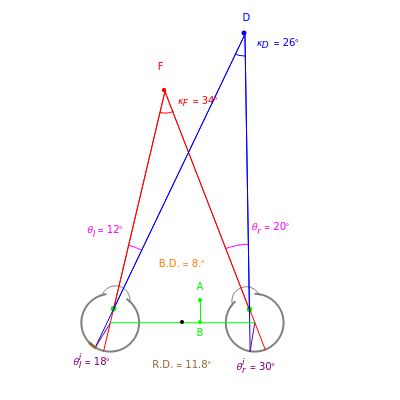
This Demonstration shows binocular and retinal disparity. Since our eyes are separated, they receive slightly different images, a "disparity". Mathematically, binocular disparity is the difference between the "convergence angles" . Binocular disparity is shown in degrees in orange. The scale is very small to exaggerate the angles in order to see what they measure at normal viewing distances.
B.D.=-
κ
F
κ
D
Simple geometry shows that binocular disparity is also the signed difference of the separation angles measured counterclockwise from distraction to fixate for the two eyes, . With these sign conventions, the formula works in all cases.
θ
B.D.=-=-
κ
F
κ
D
θ
r
θ
l
θ
The term "binocular disparity" refers to geometric measurements made external to the eye. The disparity of the images on the actual retina depends on factors internal to the eye, especially the location of the nodal points, even if the cross section of the retina is a perfect circle as in the model. The small brown segment shows the disparity between the images of the left and right eye. Notice that retinal disparity depends on the node location by sliding the "node percent" slider.