Bingham Fluid Flow in a Circular Tube

yield stress

0.15

zero-shear viscosity

0.05

A Bingham fluid acts like a rigid body at low shear stress but flows like a viscous fluid at high shear.

Consider the laminar flow of a Bingham fluid in a long circular tube of radius

R=0.01m

and length

L=1m

. The fluid flows under the influence of a pressure difference

ΔP=100N/

2

m

. The fluid density is

ρ=0.75kg/l

.

One can derive an analytical expression for the velocity, given by http://www.syvum.com/cgi/online/serve.cgi/eng/fluid/fluid807.html:

v

z

=

ΔP

2

R

4

μ

0

L

1-

2

r

R

-

τ

0

R

μ

0

1-

r

R

for

R⩾r⩾

r

0

,

v

z

=

ΔP

2

R

4

μ

0

L

1-

2

r

0

R

for

r⩽

r

0

,

where

r

0

=

2L

τ

0

ΔP

.

The mass flow rate is given by:

w=

R

∫

0

2πρr

v

z

dr=

ΔP

4

R

ρπ

8

μ

0

L

1-

4

τ

0

3

τ

R

+

1

3

4

τ

0

τ

R

, with

τ

R

=

ΔPR

2L

.

Here

μ

0

is the zero–shear viscosity and

τ

0

is the yield stress. You can vary these two parameters.

For a Newtonian fluid, the mass flow rate is given by the Hagen–Poiseuille equation:

w=

ΔP

4

R

ρπ

8μL

.

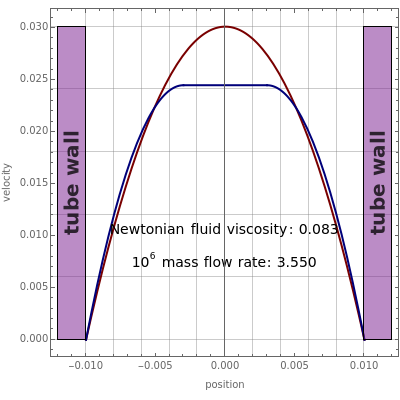
This Demonstration plots the velocity profile (blue curve) and gives the value of the corresponding mass flow rate. In addition, the velocity profile for a Newtonian fluid is plotted (red curve). The viscosity,

μ

, of the Newtonian fluid is chosen such that both fluid mass flow rates are equal. The value of the viscosity,

μ

, is also shown.