Asymptotic Stability of Dynamical System by Lyapunov's Direct Method

Consider the two-dimensional autonomous dynamical system:

x

t

=y

,

y

t

=-2bx-3

2

x

-ay

.

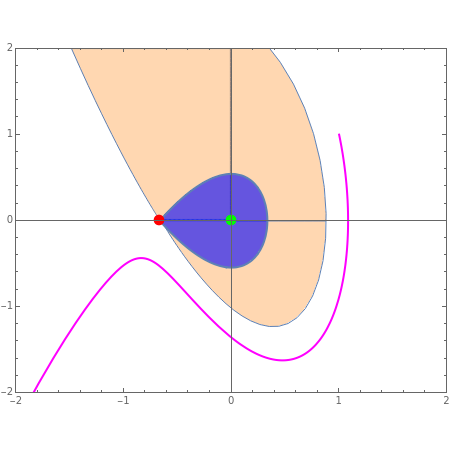
There are two steady states,

S

1

=(0,0)

and

S

2

=(-2b/3,0)

, shown by the green and red points.

Restricting the parameters to

a=1

and

b=1

, we compute and plot the region of asymptotic stability, shown in orange. All trajectories originating at an initial condition (IC) chosen in this orange region end at the

S

1

. Trajectories diverge otherwise. The blue region is also a basin of attraction for

S

1

. This region is obtained using Lyapunov's direct method and the Lyapunov function

V(x,y)=b

2

x

+

3

x

+

2

y

2

. The blue region cannot contain

S

2

because it is an unstable steady state.

V=K

defines a closed curve containing the origin if

K

is a positive constant. The largest such region can be obtained by having

S

2

at its frontier, or

K=4

3

b

/27

. You can drag the locator to change the IC.