Area under a Parabola by Symmetries

transform region

scale region

1.

show labels

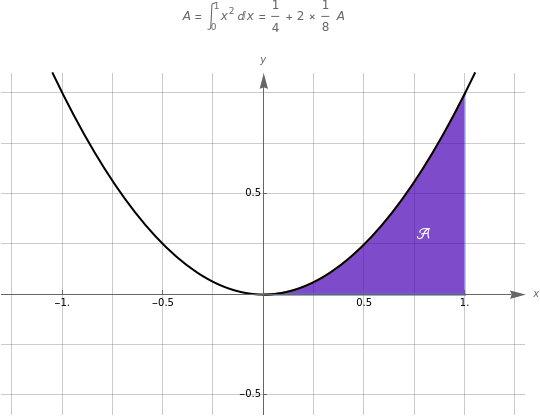
The area

A

of the region



under the curve

y=

2

x

over the interval

[0,1]

equals the area of the region

ℬ

(in light blue) under the curve and above the line

y=x-1/2

. The area-preserving shear-translation symmetry

(x,y)↦x-

1

2

,y-x+

1

4

of the curve moves the region

ℬ

to a region whose area is one-quarter plus twice the area of the region



under the curve over the interval

[0,1/2]

. The scaling symmetry

(x,y)↦

1

2

x,

1

4

y

of the curve maps



to



and reduces the area by the factor

1/8

. Thus

A=

1

4

+2×

1

8

A

so

A=1/3

.