Approximating the Derivatives of a Function Using Chebyshev-Gauss-Lobatto Points
Approximating the Derivatives of a Function Using Chebyshev-Gauss-Lobatto Points
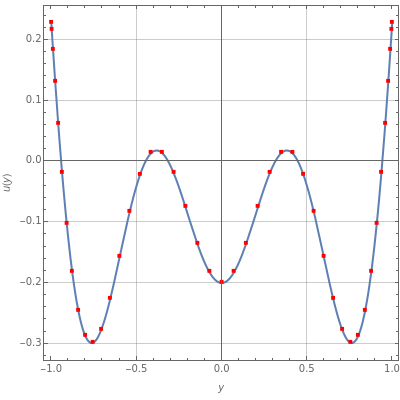
Consider the function defined by . Using the Chebyshev–Gauss–Lobatto points, it is possible to approximate the values of the two first derivatives of at these points.
u(y)=cos(5y)-15
2
y
u(y)
This Demonstration plots , , and , as well as the error made if the first- and second-order derivatives of are approximated using Chebyshev–Gauss–Lobatto points.
u(y)
u'(y)
u''(y)
u(y)
As you increase the number of interior points , you can see how the error (e.g., for given by ) becomes insignificant.
N
u'
u'()-
y
i
u'
i,approximate