An Illustration of the Central Limit Theorem Using Chi-Square Samples
An Illustration of the Central Limit Theorem Using Chi-Square Samples
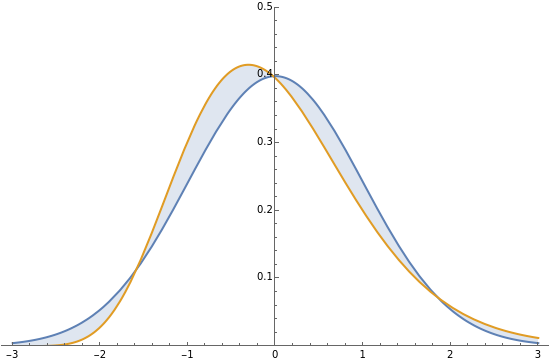
If ,,…, is a random sample from a distribution with finite mean and variance , then the central limit theorem asserts that the density function of -μ approaches a standard normal density as . If the underlying distribution is a distribution with one degree of freedom, the density function of -μ can be derived exactly (see the details). This Demonstration compares that density (purple) with a standard normal density (blue) for various values of .
X
1
X
2
X
n
μ
2
σ
X
σ
n
n→∞
2
χ
X
σ
n
n