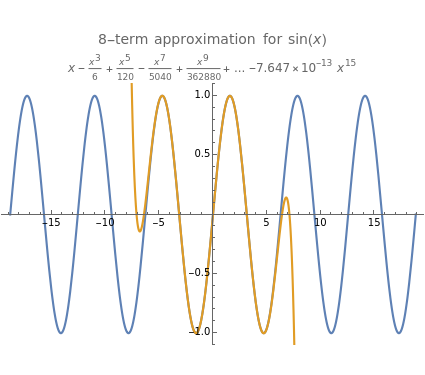
Accuracy of Series Approximations

select function

sin(x)

x range

number of terms

8

In physics and mathematics, series expansions to approximate functions are often used because using the exact solution is either impossible or involves unnecessary complicated calculations. This Demonstration shows how accurate the series expansions for

sin(x)

,

cos(x)

,

-x



,

-

2

x



, and

sinc(x)

are, and how adding terms increases that accuracy moving away from the origin.