A Wave Collapse in the Causal Interpretation of Quantum Theory
A Wave Collapse in the Causal Interpretation of Quantum Theory
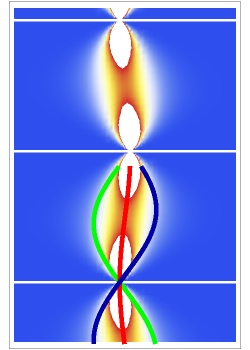
A central consequence of the causal interpretation (CI) is that trajectories do not cross [2, 3]. But what happens to the motion of quantum particles if the wavefunction becomes singular and indefinite? Here, an example is presented for the Gross–Pitaevskii equation with a harmonic potential and a time-dependent nonlinear potential. At certain time steps, where , the squared wavefunction becomes infinitely large and in an infinitesimal region and a singularity occurs.
sec(Ωt+δ)=0
In the causal interpretation, every particle has a definite position and momentum at all times. The trajectories within the wavepacket are not directly measurable but are guided by a quantum potential. Both quantities could be derived from the wavefunction.
In general, crossing trajectories are possible only for multivalued phase functions or for multidimensional fields, in which the orbits in the phase space are mapped into the lower-dimensional configuration space [2].
In the case of an indefinite wavefunction, the gradient of the phase function becomes multivalued and the trajectories can cross. The particle, which starts to the left of the peak of the wavefunction, would be found on the right side of the peak after the singularity. For these very special cases the motion of trajectories does not describe a deterministic process, because the wavefunction is irregular. Thus it must be kept in mind that this is an artificial model of a dynamic system, because the equation of the trajectories is derived from a wavefunction that is not completely definite in -space. But, roughly speaking, one could attempt to interpret the term in the Gross–Pitaevskii equation as a potential term for a measuring device that detects the position of a particle at certain times , with , which introduces a certain type of wave collapse.
(x,t)
sec(Ωt+δ)(u)
*
u
t=
πn-2δ
2Ω
n=1,3,5,…
The graphic on the left shows the density (blue), the velocity (gray), and the quantum potential (red). On the right, you can see the density and the trajectories in -space.
(x,t)