A Parallelogram Defined by the Centers of Four Circumcircles
A Parallelogram Defined by the Centers of Four Circumcircles
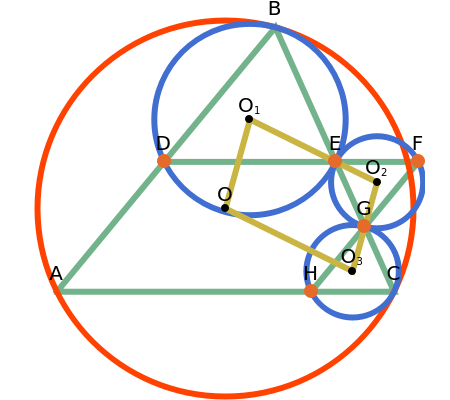
Let ABC be a triangle. Let the line DE be parallel to AC with D on AB and E on BC. Let the line GH be parallel to AB with H on AC and G on BC. Let F be the intersection of DE and GH. Let O, , , and be the circumcircles of the triangles ABC, DBE, FEG, and CGH, respectively. Then is a parallelogram.
O
1
O
2
O
3
OO
1
O
2
O
3