A Noncontinuous Limit of a Sequence of Continuous Functions
A Noncontinuous Limit of a Sequence of Continuous Functions
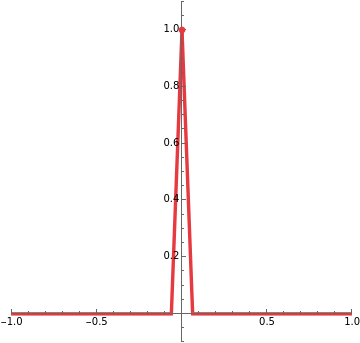
Consider a sequence of continuous real-valued functions of a real variable. The sequence converges pointwise on a set to a function if for each in , (x)f(x) as . The limit is not guaranteed to be continuous; in this Demonstration the limit has a removable discontinuity. (To construct a limit that is discontinuous everywhere in , construct with spikes at all numbers that can be written in the form , where and are positive integers and .)
f
n
f
n
E
f
x
E
f
n
n∞
f
[0,1]
f
n
p/q
p
q
p<q≤n
The limit of a uniformly convergent sequence of continuous functions is guaranteed to be continuous. Here "uniformly" means that in the ϵ- definition of the limit, the same must apply to every in . Pointwise convergence only requires an that may depend on .
N
N
x
E
N
x