A Differential Equation for Heat Transfer According to Newton's Law of Cooling

proportionality constant k

1.5

initial temperature T(0) of surroundings

60

Let

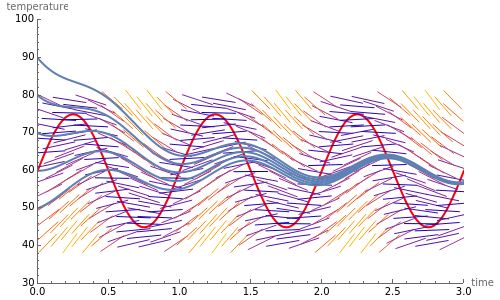
u(t)

be the temperature of a building (with neither heat nor air conditioning running) at time

t

and let

T(t)

be the temperature of the surrounding air. Newton's law of cooling states that

du

dt

=-k(u-T(t))

,

where

k

is a constant independent of time.

In this example,

T(t)=T(0)+15sin(2πt)

is plotted in red;

T(0)

is the initial temperature of the air surrounding the building. The value of

k

depends on a number of factors including the insulation of the building. In this example, you can modify the proportionality constant and mean temperature.

Five specific solutions around the initial temperature are plotted as solid blue curves through the dashed blue lines that represent the direction fields.