A Concurrency from Midpoints of Arcs of the Circumcircle
A Concurrency from Midpoints of Arcs of the Circumcircle
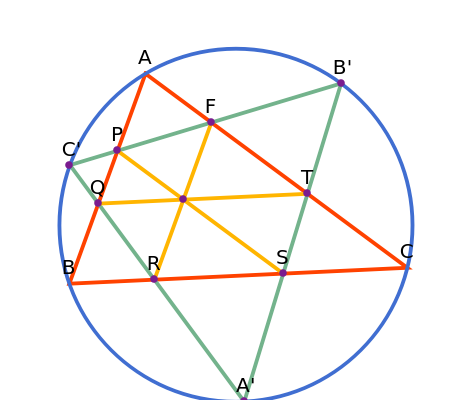
Let ABC be a triangle. Let A', B', and C' be the midpoints of the arcs BC, CA, and AB of the circumcircle of ABC, respectively. Let A'B' meet BC and AC at S and T, B'C' meet AC and AB at F and P, and C'A' meet AB and BC at Q and R. Then PS, QT, and FR are concurrent.