1. Ambiguous Rings
1. Ambiguous Rings
This Demonstration explores ambiguous rings.
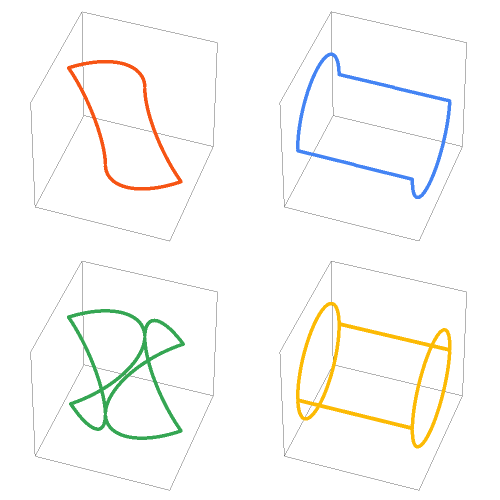
An ambiguous ring is a three-dimensional composite space curve that can be viewed as a circle, a polygon, or a shape like a lemniscate or the letter S, depending on the viewpoint.
Such a ring or ring-set can be defined as the intersection curve of a circular cylinder ring and a polygonal cylinder (a prism) with the same radius or circumradius and intersecting at a right angle.
This Demonstration considers intersections of a circular cylinder with triangular, square, pentagonal and hexagonal cylinders. For each case, closed curves are possible when there is an exact fit of the polygonal cross section inside the circular cylinder. These specific settings for the circumradius, axial rotation and axial offset of the polygonal cylinder can be derived by using the Wolfram Demonstration Intersection of Circular and Polygonal Cylinders.