13. Construct a Triangle Given the Length of Its Base, the Difference of the Base Angles and the Difference of the Lengths of the Other Two Sides

d

δ

c

step 1

step 2

This Demonstration shows a construction of a triangle

ABC

given the length

c

of the base

AB

, the difference

d

of the lengths of the other two sides

BC

and

CA

, and the difference

δ

of angles at the base.

Construction

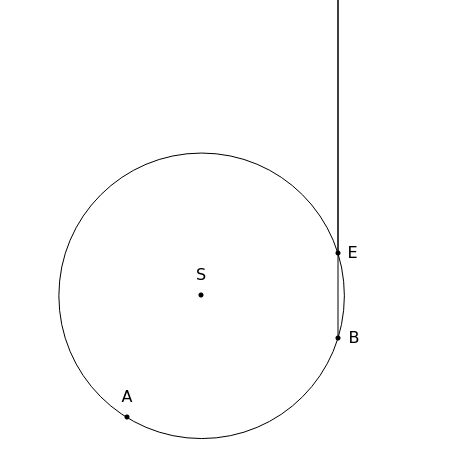
Step 1: Draw a line

BE

of length

d

and a circle with center

S

and central angle

δ

over the chord

BE

. Measure out the point

A

on the circle at distance

c

from

B

.

Step 2: Let the point

C

be the intersection of

BE

and the right bisector of

AE

.

Then

ABC

satisfies the given conditions.

Verification

Let

∠CAB=α

and

∠ABC=β

.

By construction,

AB=c

. By step 2,

CA=CE

, so

d=BE=BC-CE=BC-CA

, the difference of the other sides.

Since the central angle

∠ESB=δ

by construction,

∠EAB=δ/2

. The line

DC

bisects the angle at

C

. In any triangle, the

∠DEC=∠DAC=α

,

∠EDB=α-β

; since

ADE

is isosceles,

∠EAB=(α-β)/2

. So

δ/2=(α-β)/2

and

δ=α-β

.