Derive Hessian for matrix function
Derive Hessian for matrix function
Util
Util
(*ChangeTensorProducttoactlikeKroneckerproduct*)Unprotect[TensorProduct];TensorProduct=KroneckerProduct;Protect[TensorProduct];On[Assert];(*columnvectorize,followingMagnus,1999*)vectorize[W_]:=Transpose@{Flatten@Transpose[W]};unvectorize[Wf_,rows_]:=Transpose[Flatten/@Partition[Wf,rows]];toscalar[v_]:=Block[{t},t=Flatten@v;Assert[Length[t]1];First@t];vec=vectorize;unvec=unvectorize;v2c[c_]:=Transpose[{c}](*turnsvectortocolumnmatrix*)c2v[c_]:=Flatten[c](*turnscolumnmatrixintovector*)(*Partitionsmatrixintoblocks{{axa,axb},{bxa,bxb}}*)partitionMatrix[mat_,{a_,b_}]:=Module[{},Assert[a+bLength@mat];Assert;[a+bLength@mat];Internal`PartitionRagged[mat,{{a,b},{a,b}}]];(*Commutationmatrixm,n*)Kmat[m_,n_]:=Module[{x},X=Array[x,{m,n}];before=Flatten@vectorize@X;after=Flatten@vectorize@Transpose[X];positions=MapIndexed[{First@#2,First@Flatten@Position[before,#]}&,after];matrix=SparseArray[#1&/@positions]]
Setup the problem
Setup the problem
(*runutil.nb*)Clear[a,b];f1=2;f2=3;f3=4;Asize=f1f2;Bsize=f2f3;A=Array[a,{f1,f2}];B=Array[b,{f2,f3}];var={A,B};l[{A_,B_}]:=Tr[(A.B).(A.B)];(*Lossinflattenedrepresentation*)flatten[{A_,B_}]:=c2v[vectorize[A]~Join~vectorize[B]];unflatten[W_]:=Module[{},Aflat=v2c@W[[;;Asize]];Bflat=v2c@W[[Asize+1;;]];{unvectorize[Aflat,f1],unvectorize[Bflat,f2]}];varf=flatten[{A,B}];lf[vals_]:=l[unflatten[vals]];
Gradients
Gradients
gradA=2A.B.B;gradB=2A.A.B;grad={gradA,gradB};gradf=flatten[grad];D[lf[varf],{varf,1}]==gradf//Simplify
True
Hessians
Hessians
H=D[lf[varf],{varf,2}];(*hessian*)(*replaceallvalueswith1's*)sub1:=Thread[varfArray[1&,Length@varf]];(*replaceallvaluesinAwith1'ss,Bwith2's*)sub2:=Module[{subv,alist,blist,avals,bvals},subv[var_,vals_]:=Thread[varvals];alist=varf[[;;f1f2]];blist=varf[[f1f2+1;;]];avals=Array[1&,{f1f2}];bvals=Array[2&,{f2f3}];subv[alist,avals]~Join~subv[blist,bvals]]{{Haa,Hab},{Hba,Hbb}}=partitionMatrix[H,{f1f2,f2f3}];
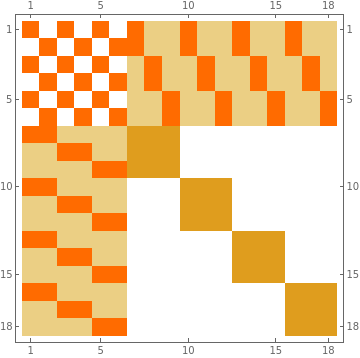
(H/.sub1)//MatrixPlot
Haa==2(B.B)IdentityMatrix[{f1,f1}]//Simplify
True
Hbb2IdentityMatrix[{f3,f3}](A.A)//Simplify
True
Hab2BA+2IdentityMatrix[3](A.B).Kmat[3,4]//Simplify
True
Hba2((B.A)IdentityMatrix[3]).Kmat[2,3]+2(BA)//Simplify
True