In[]:=
Sun 7 May 2023 19:55:31
Checking Ulrich’s FixedPoint solution
Checking Ulrich’s FixedPoint solution
Ulrich’s fixed solution for p=2
Ulrich’s fixed solution for p=2
In[]:=
ClearAll["Global`*"];h=1/(1+#)^2&;a=-2;b=1;inf=10000;(*~Infinity*)nl=NestList[Function[{fa},Block[{int,x,t},int[t_?NumericQ]:=Block[{z},NIntegrate[h[z]fa[z,t],{z,0,inf(*Infinity*)},Method->{Automatic,"SymbolicProcessing"->0}]];NDSolveValue[{Derivative[0,1][f][x,t]==ah[x]f[x,t]+bh[x]int[t],f[x,0]==1},f,{x,0,inf},{t,0,10},MaxStepSize->{100,Automatic}]]],1&(*Identity*),10];Plot3D[h[x]nl[[-1]][x,t],{x,0,10},{t,0,10},PlotRange->All,MeshFunctions->{#3&},AxesLabel->{x,t,f[x,t]}]
Out[]=
Check against manual solution by DinosaurEgg
Check against manual solution by DinosaurEgg
In[]:=
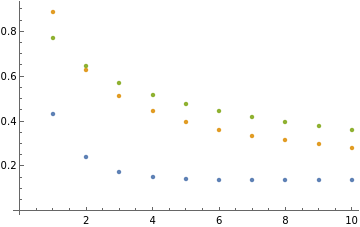
lossVal[t_]:=Module[{x},obj=h[x]nl[[-1]][x,t];NIntegrate[obj,{x,0,inf}]];tvals=Table[t,{t,1.,10}];ulrichVals=Table[lossVal[t],{t,tvals}];Clear[i,s];x=+1+ArcTan[x];gdVals=Table,{t,tvals};dinasaurEggVals=TableInverseLaplaceTransform1+ArcTan[x],s,t,{t,tvals};ListPlot[{ulrichVals,gdVals,dinasaurEggVals},PlotLegends->{"ulrich","gd","dinasaurEgg"}]
2/s
;i=10;expr=2
(i+1)
2+s
2
(i+1)
1
s+2
2
(i+1)
ArcTan[x]
1
x
1
x
Pi
4t
ArcTan[x]
1
x
1
x
Out[]=
Older stuff
Older stuff