https://math.stackexchange.com/questions/4648662/minimizing-frac-operatornametrh22-operatornametrh3-operatorname
In[]:=
Thu 9 Mar 2023 16:15:19
Single step of Gradient Descent
Single step of Gradient Descent
What quadratic results in least progress in terms of loss reduction for gradient descent?https://math.stackexchange.com/questions/4648662/minimizing-frac-operatornametrh22-operatornametrh3-operatornameTLDR; efficiency drops as , greedy step size is asymptotically 3x more efficient than LipshitzFor single step error drop, see: https://www.wolframcloud.com/obj/yaroslavvb/nn-linear/forum-step1-minimizer.nb
1
d
Util
Util
In[]:=
rsort[l_]:=Reverse[Sort[l]];traceNormalize[h_]:=;nf[x_]:=NumberForm[N[x],{3,3}];SF=StringForm;On[Assert];
h
Total[h]
Greedy step size
Greedy step size
Lipschitz drop: Tr()Greedy drop: Tr()
1
||H||
2
H
Tr()
2
H
Tr()Tr(H)
3
H
2
H
Numeric minimization
Numeric minimization
In[]:=
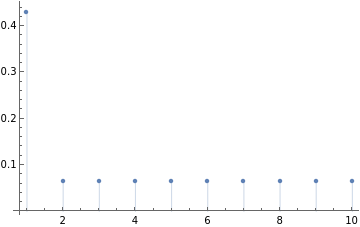
Clear[h];d0=10;Block{d=d0},d=10;hvec=Array[h,d];obj=;poscons=hvec>0;sol=NMinimize[{obj,hvec>0},hvec];hh=rsort@traceNormalize[hvec/.Last@sol];Print["Largest eval: ",nf@Max[hh],", other eval: ",nf@Min[hh]];ListPlot[hh,PlotRange->All,Filling->Axis]
2
Tr[hvec*hvec]
Tr[hvec*hvec*hvec]Tr[hvec]
Largest eval: 0.430, other eval: 0.063
Out[]=
Nicer syntax but less robust
Nicer syntax but less robust
In[]:=
sol=NMinimize,c∈Simplex@IdentityMatrix[d0];Print["Δloss: ",nf@First@sol];Print[SF["d=``, h=``",d0,rsort[nf/@(c/.Last@sol)]]]
2
Tr[c*c]
Tr[c*c*c]
Δloss: 0.597
d=10, h={0.430,0.063,0.063,0.063,0.063,0.063,0.063,0.063,0.063,0.063}
user1551 solution
user1551 solution
In[]:=
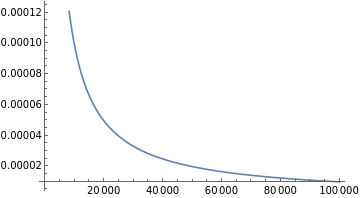
Clear[d,lambda2,xd,xk,lossDrop,worstLossDrop];d0=10;lambda2=1+2ArcCos;xd0=;xk0=;lossDrop=;worstLossDrop=lossDrop/.{xd->xd0,xk->xk0};Block[{d=d0},Print["Eigenvalues normalized: ",xd+(d-1)xk==1/.Thread[{xd,xk}->{xd0,xk0}]];Print[SF["Top eval for d=`` is ``",d,nf[xd0]]];Print[SF["Other eval for d=`` is ``",d,nf[xk0]]];Print[SF["Δloss for d=`` is ``",d,nf[worstLossDrop]]];];Plot[xk0,{d,1,100000}]Print["Top eval: ",xd0//FullSimplify];Print["Other eval: ",xk0//FullSimplify];xda=Asymptotic[xd0,{d,∞,1}];xka=Asymptotic[xk0,{d,∞,1}];Print["Asymptotic top eval: ",xda];Print["Asymptotic other eval: ",xka];asymptoticWorstLossDrop=lossDrop/.{xd->xda,xk->xka}//Simplify;asymptoticWorstLossDrop=Asymptotic[asymptoticWorstLossDrop,{d,∞,1}];Print["Asymptotic loss drop: ",asymptoticWorstLossDrop];Plot[{worstLossDrop,asymptoticWorstLossDrop},{d,1,1000},PlotLegends->{"Δloss","Δloss asympt"}]
d
Cos1
3
1
d
lambda2
lambda2+d-1
1
lambda2+d-1
2
(+(d-1))
2
xd
2
xk
(+(d-1))
3
xd
3
xk
Eigenvalues normalized: True
Top eval for d=10 is 0.430
Other eval for d=10 is 0.063
Δloss for d=10 is 0.597
Out[]=
Top eval: 1+
1-d
d+2
d
CosArcSec
d
3
Other eval:
1
d+2
d
CosArcSec
d
3
Lipschitz step size
Lipschitz step size
Ryszard solution
Ryszard solution
Greedy vs Lipschitz
Greedy vs Lipschitz
Related
Related
Related:
- Which p maximizes r for given R?
https://math.stackexchange.com/questions/4633085/bounds-on-max-i-p-i-in-terms-of-sum-i-p-i2
- how to do Convex optimization faster in Mathematica
https://mathematica.stackexchange.com/a/280128/217
- Which p maximizes r for given R?
https://math.stackexchange.com/questions/4633085/bounds-on-max-i-p-i-in-terms-of-sum-i-p-i2
- how to do Convex optimization faster in Mathematica
https://mathematica.stackexchange.com/a/280128/217