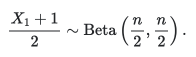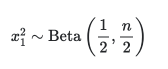In[]:=
(*deployswithcanonicalname*)deploy
Wed 21 Jun 2023 09:33:14
Distribution of a squared coordinate on a sphere
Distribution of a squared coordinate on a sphere
First and second coordinate
First and second coordinate
Regular coordinate
Regular coordinate
In[]:=
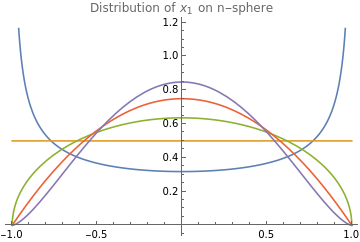
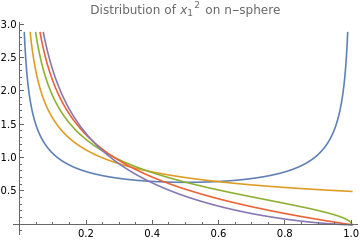
ClearAll["Globals`*"];dims=Range[5];SF=StringForm;legends=SF["n=``",#]&/@dims;func[n_]=PDF[#,x]&@TransformedDistribution[(2x-1),xBetaDistribution[n/2,n/2]]//SimplifyPlot[Evaluate[func/@dims],{x,-1,1},PlotLegends->legends,PlotLabel->"Distribution of on n-sphere"]func[n_]=Gamma;func[n_]=Refine@PDF[BetaDistribution[1/2,n/2],x];(*sameasabove*)func[n]Plot[Evaluate[func/@dims],{x,0,1},PlotLegends->legends,PlotLabel->"Distribution of on n-sphere"]
x
1
-1+
n
2
(1-x)
1+n
2
π
x
Gamman
2
2
x
1
Out[]=
1-n
2
-1+
n
2
(1-)
2
x
Beta,
n
2
n
2
Out[]=
Out[]=
-1+
n
2
(1-x)
x
Beta1
2
n
2
Out[]=
Deriving from characteristic functions
Deriving from characteristic functions
Following example in:
https://mathematica.stackexchange.com/a/286688/217
https://mathematica.stackexchange.com/a/286688/217
In[]:=
pdf=;$Assumptions={0<x<1};char=Expectation[Exp[Itx],xTransformedDistribution[(2x-1),xBetaDistribution[n/2,n/2]]];pdf2=InverseFourierTransform[char,t,x,FourierParameters->{1,1}];
n/2-1
(1-)
2
x
Beta[n/2,1/2]
In[]:=
pdf==pdf2/.{n->3,x->RandomReal[{0,1}]}
Out[]=
True
In[]:=
char=Expectation[Exp[It],xTransformedDistribution[(2x-1),xBetaDistribution[n/2,n/2]]];InverseFourierTransform[char,t,x,FourierParameters->{1,1}]
2
x
Out[]=
-1+
n
2
(1-x)
1+n
2
π
x
Gamman
2
Deriving from Mathematica built-in
Deriving from Mathematica built-in
In[]:=
n=.;dist=BetaDistribution[n/2,n/2];squaredDist=TransformedDistribution[(2x-1)^2,xdist];pdf=Refine@PDF[squaredDist,x]
Out[]=
1-n
2
-1+
n
2
(1-x)
x
Betan
2
n
2
Using moment matching
Using moment matching
In[]:=
moments={1,2,3};dist=TransformedDistribution[,xBetaDistribution[n/2,n/2]];mgf=MomentGeneratingFunction[dist,u];N@SeriesCoefficient[mgf#!,{u,0,#}]&/@momentsdata=&/@RandomPoint[Sphere[n+1],10000];Moment[data,#]&/@moments
2
(2x-1)
2
First[#]
Out[]=
{0.333333,0.2,0.142857}
Out[]=
{0.331413,0.198514,0.141643}
Fourth coordinate
Fourth coordinate
In[]:=
n=2;moments={1,2,3};dist=TransformedDistribution[,xBetaDistribution[n/2,n/2]];mgf=MomentGeneratingFunction[dist,u];N@SeriesCoefficient[-mgf#!,{u,0,#}]&/@moments
4
(2x-1)
Out[]=
{SeriesCoefficient[0.25ExpIntegralE[0.75,-1.u],{u,0.,1.}],SeriesCoefficient[0.5ExpIntegralE[0.75,-1.u],{u,0.,2.}],SeriesCoefficient[1.5ExpIntegralE[0.75,-1.u],{u,0.,3.}]}
In[]:=
data=&/@RandomPoint[Sphere[n+1],10000];Moment[data,#]&/@moments
4
First[#]
Out[]=
{0.200752,0.11119,0.0765144}
Old Stuff