In[]:=
Wed 22 Mar 2023 15:26:25
Approximating sum of entries as Trace
Approximating sum of entries as Trace
Can we approximate sum of entries of from values of where M is small rank-1 correction of diagonal matrix?
TLDR;
- Sum of entries can be written as a weighted sum of eigenvalues where weights are proportional to
=U.ones
Tr(ab) = || * (U a) * (U
- Traces and eigs of rank1 correction/original matrix are almost the same. Off-diag values are very different.
- Trace can be written as uniform-weighted sum of eigenvalues
- h-weighted sum appears to be an upper bound, while weighted is lower bound
math.SE question: sum of entries of A in terms of
background notebook: mathoverflow-DPR1-approx.nb
top level section: Diagonal + rank1
t
M
Tr()
t
M
TLDR;
- Sum of entries can be written as a weighted sum of eigenvalues where weights are proportional to
2
v
Tr(a
k
A
k
λ
b)
||
1
- Traces and eigs of rank1 correction/original matrix are almost the same. Off-diag values are very different.
- Trace can be written as uniform-weighted sum of eigenvalues
- h-weighted sum appears to be an upper bound, while
h
math.SE question: sum of entries of A in terms of
Tr()?
k
A
background notebook: mathoverflow-DPR1-approx.nb
top level section: Diagonal + rank1
In[]:=
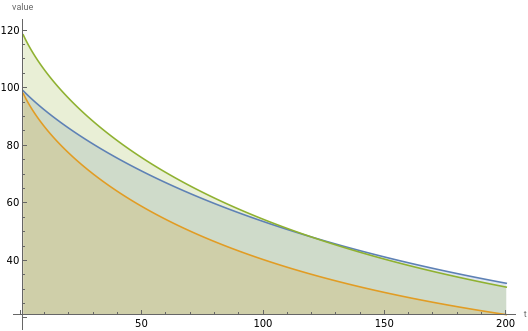
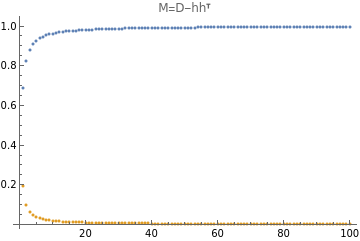
d=100;t=d;h=Table[,{i,1,d}];z=Total[h];h=h/z;II=IdentityMatrix[d];ones=ConstantArray[1.,d];(*D$isdiagonal*)A=DiagonalMatrix[2h(1-h)];B={h}.{h};(*M0isdiagonal+rank1*)M0=II-(A-B);(*Mis*)t=d;Mt=MatrixPower[M0,t];UU=Eigenvectors[M0];v=UU.ones;v2=v*v;eigs=Eigenvalues[M0];sum[x_]:=Total[x,2];DiscretePlot[{sum[MatrixPower[M0,t]],Tr[MatrixPower[M0,t]],Tr[MatrixPower[M0,t]]+*v2[[1]]},{t,1,2d},PlotLegends->{"sum of entries of ","Tr()","+Tr()"},AxesLabel->{"t","value"}]ListPlot[{Diagonal[II-A],h},PlotLegends->{"entries of D","entries of h"},PlotLabel->"M=D-hh"]sum[T_]:=Total[T,2];{N@sum[Mt],"sum of entries of Mt"}{N@Tr[Mt],"trace of Mt"}
-1.
i
t
T
t
eigs[[1]]
t
M
t
M
2
v
1
t
λ
1
t
M
Out[]=
Out[]=
Out[]=
{53.6685,sum of entries of Mt}
Out[]=
{40.4378,trace of Mt}
Write sum of entries in terms of eigenvalues
Write sum of entries in terms of eigenvalues
In[]:=
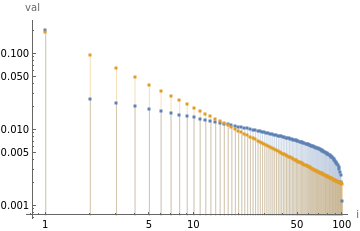
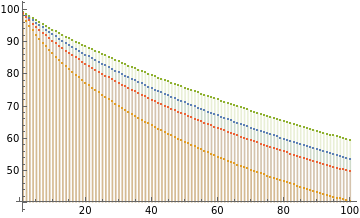
On[Assert];eigs=Eigenvalues[M0];Assert[Tr[M0]==Total[eigs]];JJ=ConstantArray[1.,{d,d}];Assert[Total[M0,2]==Tr[M0.JJ]]UU=Eigenvectors[M0];v=UU.ones;Assert[Total[M0,2]==Dot[v*v,eigs]];(*approximateequalitytesting*)DotEqual[a_,b_]:=Norm[Flatten[{a}]-Flatten[{b}],∞]<1*^-9;Assert[Dot[v*v,]≐Total[MatrixPower[M0,t],2]];(*Traceandsumarebothweightedsumofeigenvalues*)uniform=ConstantArray[1.,d]/d;Tr[MatrixPower[M0,t]]-d*Dot[,uniform];vdist=v2/Total[v2];Assert[sum[MatrixPower[M0,t]]≐d*Dot[,vdist]];nlz[v_]:=v/Total[v];ListLogLogPlot[{nlz@,h},Filling->Axis,PlotRange->All,AxesLabel->{"i","val"},PlotLegends->{"",""}]uniform=ConstantArray[1.,d]/d;Tr[MatrixPower[M0,t]]-d*Dot[,uniform];vdist=v2/Total[v2];Assert[sum[MatrixPower[M0,t]]≐d*Dot[,vdist]]DiscretePlotd*Dot[,vdist],d*Dot[,uniform],d*Dot[,h],d*Dot,nlz@,nlz[","","custom fit"
t
eigs
t
eigs
t
eigs
2
v
2
v
i
h
i
t
eigs
t
eigs
t
eigs
t
eigs
t
eigs
t
eigs
h
,{t,1,d},PlotLegends->"sum (v-weighed)","trace (uniform)","h-weighted","h
-weighted"fit=1/Sqrt[Range[d]];fit=fit/Total[fit];fit[[1]]=v2[[1]];ListLogLogPlotnlz@2
v
h
],fit,Joined->True,PlotRange->All,AxesLabel->{"i","val"},PlotLegends->"2
v
i
h
i
Out[]=
Out[]=