In[]:=
Sat 6 May 2023 18:48:12
Related questions
- Speeding up “mean time until collision” mathematica.SE post
- Expected number of non-uniform draws until collision? (symmetric polynomial solution) math.SE post
- non-uniform birthday problem Mathoverflow post (Birthday problem for non-uniform probabilities)
- more general version Mathoverflow post (Birthday problem with unequal probability: ...)
- non-uniform k-birthday problem in Mathematica post
- extreme distributions for fixed ||p|| post
- Speeding up “mean time until collision” mathematica.SE post
- Expected number of non-uniform draws until collision? (symmetric polynomial solution) math.SE post
- non-uniform birthday problem Mathoverflow post (Birthday problem for non-uniform probabilities)
- more general version Mathoverflow post (Birthday problem with unequal probability: ...)
- non-uniform k-birthday problem in Mathematica post
- extreme distributions for fixed ||p|| post
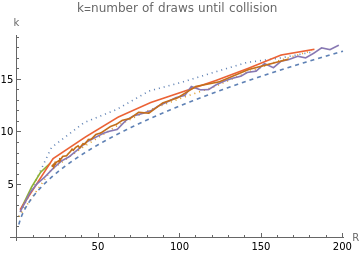
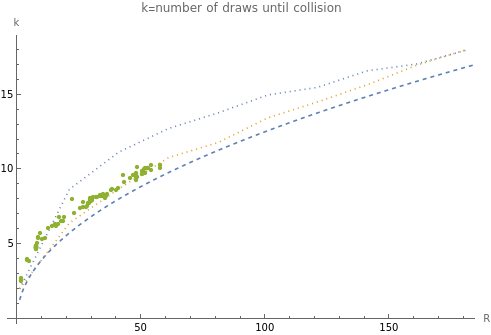
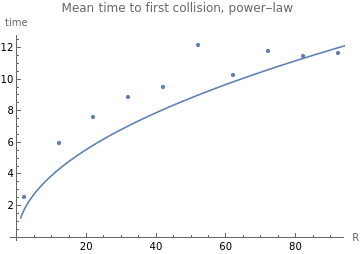
Mean-time until collision for various p
Mean-time until collision for various p
Code taken from blog-trajectories.nb
Out[]=
Add graphs
Add graphs
rmin is (huge,small,small,small,....,small) from this post
rmax is (large,medium,medium,0,0,0,....,0)
rmax is (large,medium,medium,0,0,0,....,0)
Out[]=
JimB exact solution
JimB exact solution
In[]:=
(*Generate20probabilitiesthatsumto1*)ClearAll["Global`*"];n=20;c=1;p=Table[i^(-c),{i,20}];p=p/Total[p];(*Runsimulations*)nsim=10000;s[i_]:=Sum[p[[j]]^i,{j,Length[p]}]x=RandomChoice[p->Range[Length[p]],{nsim,n+1}];mean=0;Do[k=2;While[Select[x[[i,1;;k-1]],#==x[[i,k]]&]=={}&&k<(n+1),k=k+1];mean=mean+k,{i,nsim}]mean=mean/nsim//N(*4.63702*)(*Exactmean*)kmax=Length[p]+1;2s[2]+Sum[k(k-1)MomentConvert[AugmentedSymmetricPolynomial[Join[{2},ConstantArray[1,k-2]]],"PowerSymmetricPolynomial"],{k,3,kmax}]/.PowerSymmetricPolynomial[i_]->s[i]//Expand//N(*4.63338*)
Out[]=
4.6319
Out[]=
4.63338
Old code
Old code
Slower solution
Slower solution
Out[]=