In[]:=
(*deployswithcanonicalname*)deploy:=Module[{notebookFn,parentDir,cloudFn,result},Print[DateString[]];notebookFn=FileNameSplit[NotebookFileName[]][[-1]];parentDir=FileNameSplit[NotebookFileName[]][[-2]];cloudFn=parentDir~StringJoin~"/"~StringJoin~notebookFn;result=CloudDeploy[SelectedNotebook[],CloudObject[cloudFn],Permissions"Public",SourceLinkNone];Print["Uploading to ",cloudFn];result]deploy
Tue 28 Feb 2023 12:31:10
Simulation of L1 vs L2 step sizes. Forum: https://math.stackexchange.com/questions/4647281/largest-value-of-lambda-1-in-frach-1-lambda-1-2h-1-frac-sum-i-2#4647373
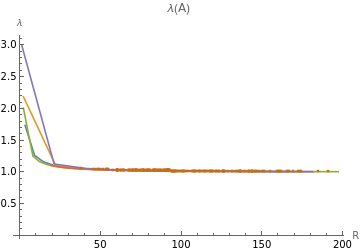
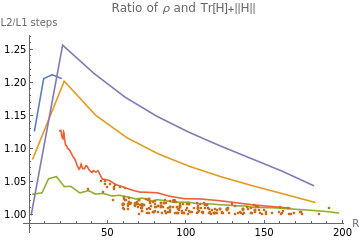
TLDR; L2 step approaches 2/Tr(H) for high dimensional matrices
TLDR; L2 step approaches 2/Tr(H) for high dimensional matrices
Util
Util
Main
Main
graph initializer (slow, 1 min)
In[]:=
graphNamesOrig=Join@@Table[GraphData[k],{k,80,200}];graphSpectraOrig=N[GraphData[#,"LaplacianSpectrum"]]&/@graphNamesOrig;graphPairs=DeleteMissing[Transpose[{graphNamesOrig,graphSpectraOrig}],1,2];Manipulate[ListPlot[graphPairs[[i,2]],PlotLabel->graphPairs[[i,1]]],{i,1,Length@graphPairs,1}]graphSpectra=graphPairs[[All,2]];
Out[]=
In[]:=
d=200;generateHarmonicSpectrum[R0_]:=With{R=Min[R0,80]},1.RangeCeiling;harmonicSpectra=generateHarmonicSpectrum/@Range[1,20,5];powerSpectra=generatePowerSpectrum[d,#]&/@Range[2,d,d/10];wishartSpectra=generateWishartSpectrum[d,#]&/@Range[2,d-1,5];linfMinSpectra=generateLinfMinSpectrum[d,#]&/@Range[1,d,d/10];linfMaxSpectra=generateLinfMaxSpectrum[d,#]&/@Range[1,d,d/10];rminSpectra=linfMaxSpectra;traceNormalize[vec_]:=;batchNormalize[vals_]:=Map[traceNormalize,vals,{-2}];{harmonicSpectra,powerSpectra,wishartSpectra,productSpectra,rminSpectra,graphSpectra}=batchNormalize[{harmonicSpectra,powerSpectra,wishartSpectra,productSpectra,rminSpectra,graphSpectra}];(*Spectraofproductsofrandommatrices.Startingwith0.95ofmax-rank,anditerating*)getIteratedProductSpectra[d_]:=Module{bd,randMat,yList,spectra},bc=Floor/.R1->0.95*d;randMat:=With[{XX=RandomVariate[NormalDistribution[],{bc,d}]},XX.XX/d];yList=NestList[randMat.#&,randMat,40];spectra=traceNormalize[]&/@yList;productSpectra=getIteratedProductSpectra[d];stepRatioPlot[ystat_,spectraGroups_,labels_]:=Module[{data,joined},joined=Table[True,Length[spectraGroups]-1]~Join~{False};data=annotateSpectra[#,spectrum2R,ystat]&/@spectraGroups;observedPlot=ListPlot[data,PlotLegends->labels,PlotRange->All,Joined->joined,AxesLabel->{"R","λ"},PlotLabel->"λ(A)"];observedPlot];stepRatioPlot&,{harmonicSpectra,powerSpectra,wishartSpectra,productSpectra,rminSpectra,graphSpectra},{"harmonic",SF["power d=``",d],SF["wishart d=``",d],SF["product d=``",d],"r-min","graph"}stepRatioPlot[ystat_,spectraGroups_,labels_]:=Module[{data,joined},joined=Table[True,Length[spectraGroups]-1]~Join~{False};data=annotateSpectra[#,spectrum2R,ystat]&/@spectraGroups;observedPlot=ListPlot[data,PlotLegends->labels,PlotRange->All,Joined->joined,AxesLabel->{"R","L2/L1 steps"},PlotLabel->"Ratio of ρ and Tr[H]+||H||"];observedPlot];stepRatioPlot&,{harmonicSpectra,powerSpectra,wishartSpectra,productSpectra,rminSpectra,graphSpectra},{"harmonic",SF["power d=``",d],SF["wishart d=``",d],SF["product d=``",d],"r-min","graph"}
π
R
6
vec
Total[vec]
-2+R1+dR1
d-R1
2
SingularValueList[#]
2
stepL2SGDfast[#]
stepL2SGDfast[#]
stepL1SGD[#]
Out[]=
Out[]=
River Li' s lower bound
River Li' s lower bound
In[]:=
Assuming{x>0,trh>2maxh>0},Solve++==1,x,Reals//NlowerBound1[h_]:=With[{maxh=Max[h],trh=Tr[h],trh2=Tr[h*h]},Root[-4+4maxhtrh2+(2maxhtrh-2trh2)#1+(-2maxh-trh)+&,2]];lowerBound2[h_]:=With[{maxh=Max[h],trh=Tr[h],trh2=Tr[h*h]},Root[-4+4maxhtrh2+(2maxhtrh-2trh2)#1+(-2maxh-trh)+&,3]];stepRatioPlot[ystat_,spectraGroups_,labels_]:=Module[{data,joined},joined=Table[True,Length[spectraGroups]-1]~Join~{False};data=annotateSpectra[#,spectrum2R,ystat]&/@spectraGroups;observedPlot=ListPlot[data,PlotLegends->labels,PlotRange->All,Joined->joined,AxesLabel->{"R","ratio of truth to bound"},PlotLabel->"Ratio of truth and River Li's lower bound"];observedPlot];stepRatioPlot&,{harmonicSpectra,powerSpectra,wishartSpectra,productSpectra,rminSpectra,linfMinSpectra,graphSpectra},{"harmonic",SF["power d=``",d],SF["wishart d=``",d],SF["product d=``",d],"r-min","r-max","graph"}
maxh
x-2maxh
trh-maxh
x
2(trh2-)
2
maxh
2
x
3
maxh
2
#1
3
#1
3
maxh
2
#1
3
#1
2
stepL2SGDfast[#]
Max[lowerBound1[#],lowerBound2[#]]
Out[]=
Ratios of λ and 2(1+ρ)
Ratios of λ and 2(1+ρ)