Eigenvalues of projected Gaussian

What happens to covariance eigenvalues if we normalize examples by length?dherrera gives nice formula in this answer:- Covariance of

x

∥x∥

for Gaussian x? stats.SE post

In[]:=

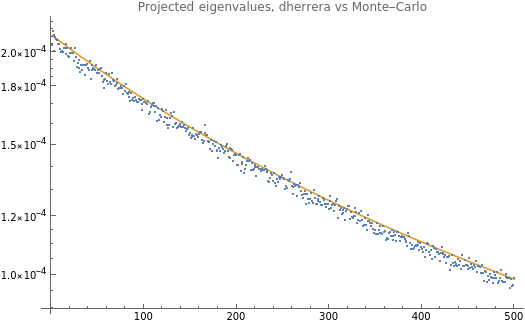
(*Gaussiansampler*)SeedRandom[1,Method->"MKL"];gaussianSampler[diag_]:=With{d=Length[diag]},Compile{{n,_Integer}},Module{vals,diagSqrt},diagSqrt=

diag

;vals=diagSqrt*#&/@RandomVariate[NormalDistribution[],{n,d}];normalizedGaussianSampler[diag_]:=With{d=Length[diag]},Compile{{n,_Integer}},Module{vals,diagSqrt},diagSqrt=

diag

;vals=Sqrt[diag]*#&/@RandomVariate[NormalDistribution[],{n,d}];#Sqrt[Total[#*#]]&/@vals;(*givensampler,computecoordinatevariances*)getDiag[sampler_,m_]:=With[{data=sampler[m]},Mean[data*data]];(*setsuptrace-normalizedzero-centeredGaussianwithp-powerlawdecayinddimensionsSide-effects:h--eigenvaluesoforiginalGaussianhp--eigenvaluesofprojectedGaussian,estimatedusingMonte-Carlod--dimensions*)setupPowerlawGaussian[d0_,p0_,m_]:=(d=d0;p=N[p0];h=Table[

-p

i

,{i,1,d}];h=h/Total[h];hp=getDiag[normalizedGaussianSampler[h],m];);(*sumofsquaresofrelativeerrors*)getError[predicted_,true_]:=With[{r=(predicted-true)/predicted},Total[r*r]];(*computetailerror*)getTail[val_]:=With[{tailLength=Ceiling[Length[val]/2]},val[[-tailLength;;]]];getTailError[predicted_,true_]:=getError[getTail@predicted,getTail@true];getErrors[predicted_,true_]:={getError[predicted,true],getTailError[predicted,true]};d=1000;p=1.1;m=10000;nf[val_]:=NumberForm[N@val,{3,3}];setupPowerlawGaussian[d,p,m];herrera=h(1+2Tr[

2

h

])-2

2

h

;herreraAdj=h(1+1.7Tr[

2

h

])-2

2

h

;ListLogPlot[{getTail[hp],getTail[h(1+2Tr[

2

h

])-2

2

h

]},Joined->{False,True},PlotStyle->PointSize[Small],PlotLabel->"Projected eigenvalues, dherrera vs Monte-Carlo",PlotLegends->{"observed",HoldForm[h(1+2Tr[

2

h

])-2

2

h

]}]

Out[]=

	observed
	h(1+2Tr[ 2 h ])-2 2 h

In[]:=

SF=StringForm;Print[SF["dimensions=``, p-decay=``, num-samples=``",d,nf@p,m]]TableForm[{nf/@getErrors[hp,h],nf/@getErrors[hp,herrera],nf/@getErrors[hp,herreraAdj]},,TableHeadings->{{"naive","herrera","adjusted"},{"error","tail error"}}]

dimensions=1000, p-decay=1.100, num-samples=10000

Out[]//TableForm=

	error	tail error
naive	5.380	2.790
herrera	0.485	0.219
adjusted	0.230	0.103