In[]:=
Thu 4 May 2023 00:37:38
Approximating DPR1 eigenvalues
Approximating DPR1 eigenvalues
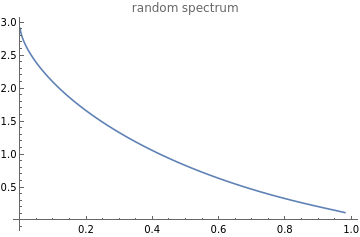
Spectrum of a large random matrix becomes deterministic, hence use the “canonical” spectrum
Sanity check of Marchenko-Pastur
Sanity check of Marchenko-Pastur
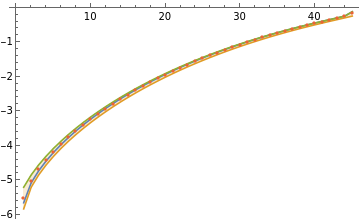
DPR1 spectrum
DPR1 spectrum
In[]:=
ClearAll["Global`*"];eigMagnitude=InverseCDF[MarchenkoPasturDistribution[.5],y]/.y->1-x;Plot@@{eigMagnitude,{x,0,1},PlotLabel->"random spectrum"}
Out[]=
In[]:=
numSamples=45;eigs=Table[eigMagnitude,{x,0,1,1./numSamples}];dpr1=Rest@Eigenvalues[-2DiagonalMatrix[eigs]+{eigs}.{eigs}];ListPlot[{dpr1,-2Most[eigs],-2Rest[eigs],-Total/@Partition[eigs,2,1]},Filling->{2->{3}},Joined->{True,True,True,False},PlotLegends->{"True","Upper","Lower","Average"}]
Out[]=
In[]:=
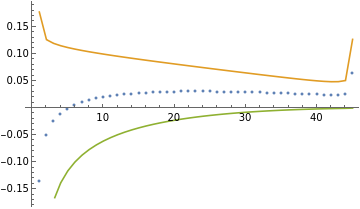
ListPlot[{dpr1+Total/@Partition[eigs,2,1],dpr1+2Most[eigs],dpr1+2Rest[eigs]},Joined->{False,True,True},PlotLegends->{"average","upper","lower"}]
Out[]=