Wolfram Cloud Document

In[]:=

SetDelayed[

]

;deploy

Sat 6 May 2023 15:45:39

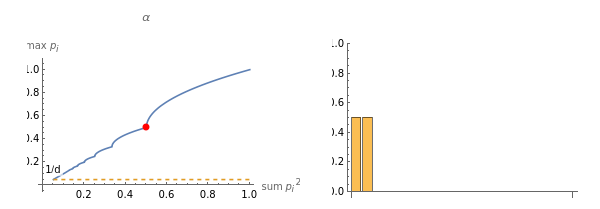
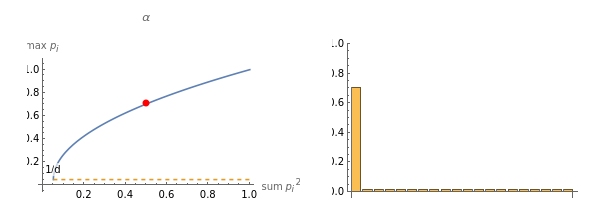
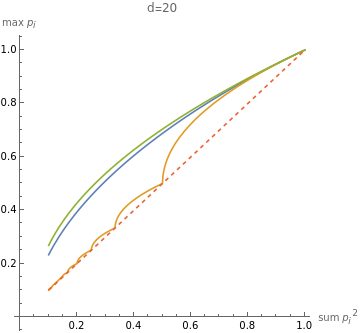
Three different spectra generated to match given rho, d constraints.Power spectrum,

||.

||

∞

minimizer,

||.

||

∞

maximizer

Posts:- Bounds on max_i p_i in terms of sum_i

2

p_i

math.se postNotebook:- forum-mean-time-to-collision.nb: using these for non-uniform “time until collision”

In[]:=

d=20;(**Seemsveryslowwhenusedinplots,needtodebugthis***)(*givenρ(sameas||p

2

||

)between1/dand1,producematchingnormalizedspectruminddimensions*)powerSpectrum[rho_,d_]:=Module{h,R,dd,decay},Assertrho>=

1

d

,"impossible rho setting, too small";Assert[rho<=1.,"impossible rho setting, too large"];R=

1

rho

;decay=IfR<1.001,100.,dd/.FindRoot

2

HarmonicNumber[d,dd]

HarmonicNumber[d,2dd]

==R,{dd,2,0,100};h=Table[

-decay

i

,{i,1,d}];hTotal[h];(*valuesfromhttps://math.stackexchange.com/a/4635453/998*)linfMinHelper[rho_,d_]:=Module{m,alpha,beta,midterm,minimizer,maximizer},m=Floor

1

rho

+1;alpha=

1

m

+

1

m

mrho-1

m-1

;beta=

1

d

+

rho-

rho

d

-

1

d

+

1

2

d

;midterm=

1

m

-

rho-

rho

m

-

1

m

+

1

2

m

;minimizer=Table[alpha,{m-1}]~Join~{midterm}~Join~Table[0,{d-m}];maximizer={beta}~Join~Table

1

d

-

1

d

drho-1

d-1

,{d-1};{minimizer,maximizer};linfMin[rho_,d_]:=First[linfMinHelper[rho,d]];linfMax[rho_,d_]:=Last[linfMinHelper[rho,d]];(*GeneratespectrumwithgivenR,dthatminimizeormaximizestablestepsize*)generateLinfMinSpectrum[R_,d_]:=linfMin[1/R,d];generateLinfMaxSpectrum[R_,d_]:=linfMax[1/R,d];annotatedPlot[rho0_,generator_,plotLabel_]:=Plot{Max[generator[rho,d]],Labeled[1/d,"1/d",Left]},rho,

1

d

,1,AxesLabel->{"sum

2

p

i

","max

p

i

"},PlotLabel->StringForm[plotLabel],AxesOrigin->{0,0},PlotStyle->{Automatic,Dashed},Epilog->{PointSize[Large],Red,Point[{rho0,Max[generator[rho0,d]]}]};annotatedDistPlot[s0_,generator_]:=(BarChart[generator[s0,d],PlotRange->{0,1}]);annotatedCombinedPlot[s0_,generator_,label_]:=GraphicsRow[{annotatedPlot[s0,generator,label],annotatedDistPlot[s0,generator]}]With[{s0=0.5},annotatedCombinedPlot[s0,linfMin,"α"]]With[{s0=0.5},annotatedCombinedPlot[s0,linfMax,"α"]]d=20;SF=StringForm;Plot[{Max@powerSpectrum[rho,d],Max@linfMin[rho,d],Max@linfMax[rho,d],rho},{rho,2/d,1},PlotLegends->{"power-law","min ||p

||

∞

","max ||p

||

∞