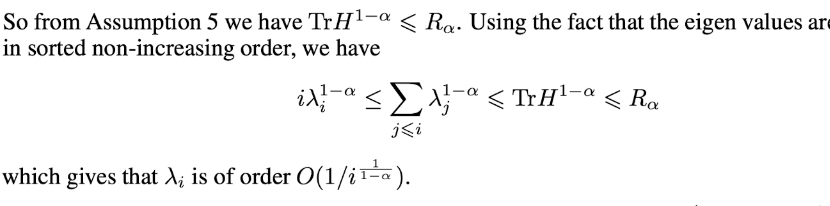In[]:=
Sun 7 May 2023 20:24:35
Alpha Capacity, Effective Rank, Power-law decay
Alpha Capacity, Effective Rank, Power-law decay
Flamarion - Last Iterate convergence, notability
In[]:=
Clear[p,r,α,a];p4α$=;r4p$=Asymptotic[Zeta[p],p1];r4α$=First@SolveValuesr-1+1,r//Simplify(*Eliminate[{p==p4α$,r==r4p$},p]*)
1
1-α
1
1-α
Out[]=
-1+
1
α
In[]:=
ClearAll["Global`*"];p4a=1/(1-a);r4p=1/(-1+p);temp=Eliminate[{p==p4a,r==r4p},p];a4r=First@SolveValues[temp,a];solve[eq_,var_]:=Print[var,"=",FullSimplify@First@SolveValues[eq,var]];solve[p==p4a,p]solve[r==r4p,r]solve[a==a4r,a]solve[p==p4a,a]solve[r==r4p,p]solve[a==a4r,r]
p=
1
1-a
r=
1
-1+p
a=
1
1+r
a=
-1+p
p
p=1+
1
r
r=-1+
1
a
In[]:=
Rfromr=Asymptotic,p->1/.p->1+;Print["R=",Rfromr]
2
Zeta[p]
Zeta[2p]
1
r
R=
6
2
r
2
π
In[]:=
Print["r=",Assuming[{r>0,R>0},First@SolveValues[Rfromr==R,r]]]
r=
π
R
6
Solution from the birthday paradox
In[]:=
Clear[d,R];Solve++2Log[2]d==
1
2
1
4
Pi
,dR
2
Out[]=
d
-
2π
R
+πR4Log[2]
≃
-0.904075
R
+1.13309RDimensions required for alpha-capacity approximation to work
Dimensions required for alpha-capacity approximation to work
TLDR; for bound of 1.5 at step=d, need
d≃
R
10
In[]:=
ClearAll["Global`*"];int=Inactive[Integrate]yExp[-ys],{y,,1};formulaLoss=Assuming[{p>1,d>1,s>1},Activate[int]]
-1/p
(y)
py
-p
(d+1)
Out[]=
-ExpIntegralE,s+ExpIntegralE,s
1
p
1-p
(1+d)
1
p
-p
(1+d)
p
In[]:=
Clear[s,d,p];Assuming[{s>1,p>1,d>1},Asymptotic[formulaLoss,{d,Infinity,1}]//Simplify]
Out[]=
-sExpIntegralE,s+Gamma
1
p
1
p
s
-1+p
p
ps
In[]:=
Asymptotic,p->1/.p->1+
2
Zeta[p]
Zeta[2p]
1
r
Out[]=
6
2
r
2
π
In[]:=
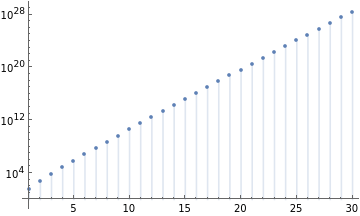
ClearAll["Global`*"];rFromR[R_]:=;lossTrue=;lossApprox=;lossApprox=Gamma-1;dimsRequiredForFidelity[p0_]:=Block[{p=p0},s0=d;(*stepcountatwhichtoevaluate*);obj=lossTrue/lossApprox/.s->s0;(*asymptoticversionisupperbound,seekatmostthisgapats0*);boundGap=3/2;d/.FindRoot[obj==1/boundGap,{d,10^10,1,10^60},WorkingPrecision->200,MaxIterations->500,PrecisionGoal->1]];dimsRequiredForFidelity[1+1/rFromR[50]]DiscretePlot[dimsRequiredForFidelity[1+1/rFromR[R]],{R,1,30,1},WorkingPrecision->20,ScalingFunctions->"Log"]
π
R
6
-ExpIntegralE,s+ExpIntegralE,s
1
p
1-p
(1+d)
1
p
-p
(1+d)
p
-sExpIntegralE,s+Gamma
1
p
1
p
s
-1+p
p
ps
1
p
-1+p
p
1
p
s
Out[]=
3.4271636860459949661268663340637041490800967717138926870859465930315609170957985086753736984667879784869029403735391456335280047227817704016607250730814234462531214420948944644798813059819151354166559×
45
10
Out[]=
Speed up
Speed up
Reuse fast compiled sampler from gd-vs-sgd
d=100,000
steps=10
B=10
1.36 sampler (1.01 after removing diagonal stuff)
0.2 MapThread
0.2 compute errors
100k per vector, 1000 steps x 10 batch = 10^9 floats, 4*10^9 = 4 GB per exp.
Lesson:
Mathematica generates about 10M random numbers per second on MacBook. About 80MB/second.
Need about 100 seconds for 100k experiment (30 seconds for B=1, 60 seconds for other contingencies)
Actual, 7.25 seconds for B=3
d=100,000
steps=10
B=10
1.36 sampler (1.01 after removing diagonal stuff)
0.2 MapThread
0.2 compute errors
100k per vector, 1000 steps x 10 batch = 10^9 floats, 4*10^9 = 4 GB per exp.
Lesson:
Mathematica generates about 10M random numbers per second on MacBook. About 80MB/second.
Need about 100 seconds for 100k experiment (30 seconds for B=1, 60 seconds for other contingencies)
Actual, 7.25 seconds for B=3
Exclude first 500 steps
Exclude first 500 steps
Berthier scratch
Berthier scratch