In[]:=
(*deployswithcanonicalname*)deploy:=Module[{notebookFn,parentDir,cloudFn,result},Print[DateString[]];notebookFn=FileNameSplit[NotebookFileName[]][[-1]];parentDir=FileNameSplit[NotebookFileName[]][[-2]];cloudFn=parentDir~StringJoin~"/"~StringJoin~notebookFn;result=CloudDeploy[SelectedNotebook[],CloudObject[cloudFn],Permissions"Public",SourceLinkNone];Print["Uploading to ",cloudFn];result];deploy
Mon 12 Sep 2022 14:42:08
In[]:=
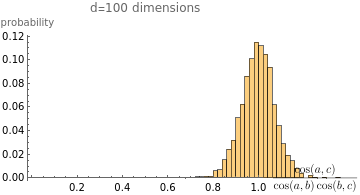
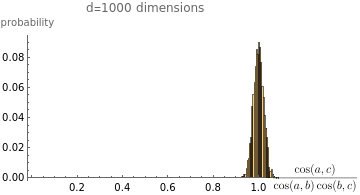
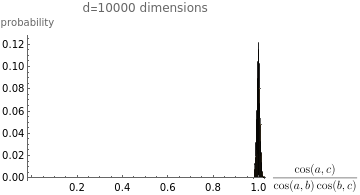
(*ResourceFunction["MaTeXInstall"][]*)<<MaTeX`;cos[vec1_,vec2_]:=;makePlot[d0_]:=d=d0;b=2000;randomBatch:=RandomVariate[NormalDistribution[],{b,d}],Automatic,"Probability",PlotRange->{{0,1},Automatic},PlotLabel->StringForm["d=`` dimensions",d],AxesLabel->{MaTeX["\\frac{\\cos(a,c)}{\\cos(a,b)\\cos(b,c)}"],"probability"};makePlot[100]makePlot[1000]makePlot[10000]
vec1.vec2
Norm[vec1]Norm[vec2]
d
;batchCos[batch1_,batch2_]:=MapThread[cos[#1,#2]&,{batch1,batch2}];A=randomBatch;B=A+randomBatch;CC=B+randomBatch;HistogrambatchCos[A,CC]
batchCos[A,B]batchCos[B,CC]
Out[]=
Out[]=
Out[]=
In[]:=
makePlot2[d0_]:=d=d0;b=10000;randomBatch:=RandomVariate[NormalDistribution[],{b,d}]
d
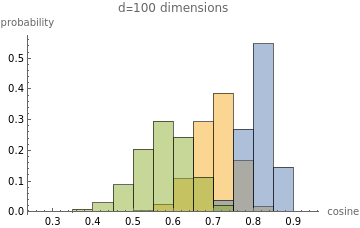
;batchCos[batch1_,batch2_]:=MapThread[cos[#1,#2]&,{batch1,batch2}];A=randomBatch;B=A+randomBatch;CC=B+randomBatch;Histogram[{batchCos[A,B],batchCos[B,CC],batchCos[A,CC]},Automatic,"Probability",PlotLabel->StringForm["d=`` dimensions",d],AxesLabel->{"cosine","probability"},ChartLegends->{MaTeX["\\cos(a,b)"],MaTeX["\\cos(b,c)"],MaTeX["\\cos(a,c)"]}];makePlot2[100]Out[]=
In[]:=
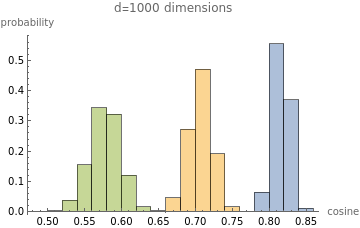
makePlot2[1000]
Out[]=
Cosines for more sums
Cosines for more sums
In[]:=
nf[num_]:=NumberForm[num,{3,3}];getSim[d0_]:=d=d0;b=4000;randomBatch:=RandomVariate[NormalDistribution[],{b,d}];cosFormat[{l1_,l2_,l3_}]:=;MapThread[StringForm["``=``",cosFormat[#1],nf@meanStat[#2]]&,{Subsets[{"a","b","c","d","e"},{3}],Subsets[{A,B,CC,DD,EE},{3}]}];TableForm@getSim[100]
d
;batchCos[batch1_,batch2_]:=MapThread[cos[#1,#2]&,{batch1,batch2}];A=randomBatch;B=A+randomBatch;CC=B+randomBatch;DD=CC+randomBatch;EE=DD+randomBatch;meanStat[{batch1_,batch2_,batch3_}]:=MeanbatchCos[batch1,batch3]
batchCos[batch1,batch2]batchCos[batch2,batch3]
StringForm["cos(``,``)",l1,l3]
StringForm["cos(``,``)",l1,l2]StringForm["cos(``,``)",l2,l3]
Out[]//TableForm=
cos(a,c) cos(a,b)cos(b,c) |
cos(a,d) cos(a,b)cos(b,d) |
cos(a,e) cos(a,b)cos(b,e) |
cos(a,d) cos(a,c)cos(c,d) |
cos(a,e) cos(a,c)cos(c,e) |
cos(a,e) cos(a,d)cos(d,e) |
cos(b,d) cos(b,c)cos(c,d) |
cos(b,e) cos(b,c)cos(c,e) |
cos(b,e) cos(b,d)cos(d,e) |
cos(c,e) cos(c,d)cos(d,e) |
Projected Gaussian
Projected Gaussian
Only add small values
Only add small values
Do random rotations instead
Do random rotations instead