In[]:=
CompoundExpression[
]
​​deploy
Tue 5 Dec 2023 17:02:24

Convergence of Gaussian SGD in high dimension

post on MathoverFlow: When is
∞
∏
i0
I-
x
i
T
x
i
0
for zero-centered Gaussian $x_i$?colab version​​

Code

In[]:=
Clear["Global`*"];​​​​(*
https://math.stackexchange.com/questions/4519054/bounds-on-spectral-radius-of-2-textdiaghh-cdot-1t
 *)​​stepL2SGDfast[h_]:=Module[{d=Length[h],normalize,step,evec},​​normalize[v_]:=v/Sqrt@Total[v*v];​​step[v_]:=2h*v+h*Total[v];​​evec=FixedPoint[normalize[step[#]]&,ConstantArray[1.,d],1000];​​2/Norm[step@evec]​​]​​​​(* Gaussian sampler with diagonal covariance *)​​SeedRandom[1,Method->"MKL"];​​SF=StringForm;​​gaussianSampler[diag_]:=With{d=Length[diag]},​​Compile{{n,_Integer}},​​Module{vals,diagSqrt},​​diagSqrt=
diag
;​​vals=diagSqrt*#&/@RandomVariate[NormalDistribution[],{n,d}];​​​​​​(* Generates plot for Gaussian SGD with cov eigenvalues
-p
1
,
-p
2
,...,
-p
d
, by using step size a *) ​​generatePlot[p_,d_,a_]:=Module[{},​​B=1000;​​numSteps=100;​​ones=ConstantArray[1.,d];​​h=Table[
-p
i
,{i,1,d}];​​sampler=gaussianSampler[h];​​W0=sampler[B];​​​​step[w_,x_]=w-a x x.w;​​batchStep[W_]:=MapThread[step,{W,sampler[B]}];​​traj=NestList[batchStep,W0,numSteps]; (* numSteps x B x d *)​​​​errorNorms2=Total[traj*traj,{3}]; (* numSteps x B *)​​numQuantiles=100;​​compress[l_]:=Quantile[l,#]&/@Range[0,1,1/numQuantiles];​​​​meanPlot=ListLinePlot[Total[errorNorms2,{2}]/B,ScalingFunctions->"Log",PlotLegends->{"mean"}];​​filling=Table[i->{numQuantiles+2-i},{i,1,numQuantiles/2}];​​distPlot=ListLinePlot[Transpose[compress/@errorNorms2],ScalingFunctions->"Log",Filling->filling,FillingStyle->Directive[​​Opacity[.1],EdgeForm[]],PlotStyle->{Directive[Gray,Thin]}];​​​​Show[distPlot,meanPlot,AxesLabel->{"t","||e
2
||
"},PlotLabel->SF["e=e-x<e,x>",d],ImageSize->Large]​​​​];

Visualization

d=1

​

In[]:=
p=1;​​d=1;​​(*1Ddivergencethreshold,seeDSP.se
post
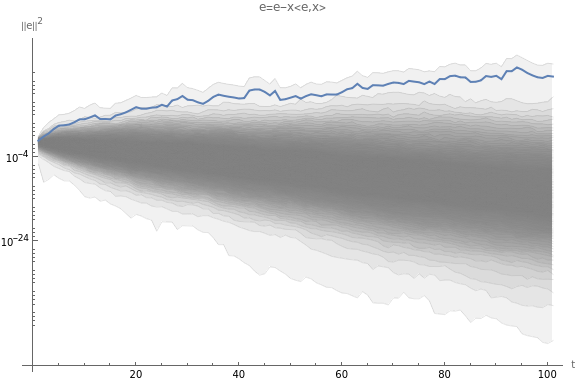
*)​​a=2.421249521036836042992780131428225933128842834067867847377838424345397835692066559296652232682365322;​​generatePlot[p,d,a*.8]​​
Out[]=
mean

d=100

In[]:=
a
Out[]=
0.336923
In[]:=
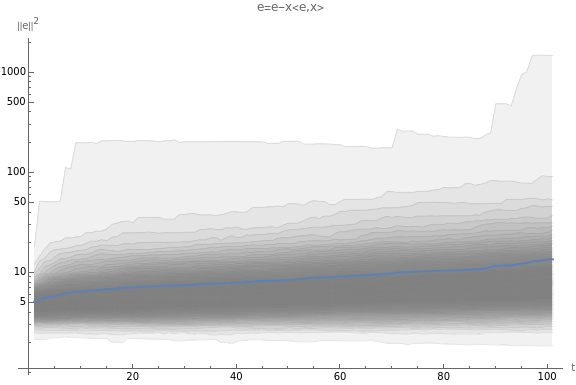
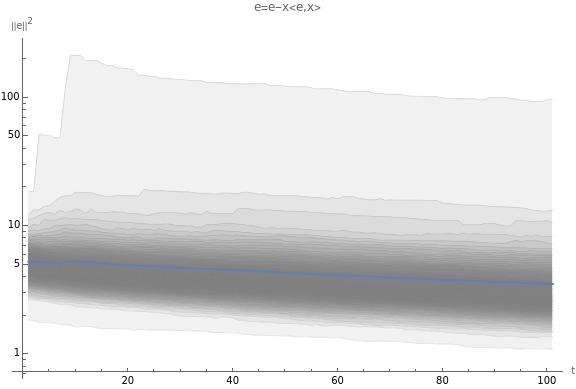
SeedRandom[1];​​p=1;​​d=100;​​a=stepL2SGDfast[Table[
-p
i
,{i,1,d}]];​​​​plot1=generatePlot[p,d,a*1.1];​​plot1​​meanErrors1={First[#],Last[#]}&@(Mean/@errorNorms2);​​plot2=generatePlot[p,d,a*0.9]​​meanErrors2={First[#],Last[#]}&@(Mean/@errorNorms2);​​SF=StringForm;​​SF["a=``",N[a,10]]​​TableForm[{meanErrors1,meanErrors2},TableHeadings->{{"a*1.1","a*.9"},{"first","last"}}]​​
Out[]=
mean
Out[]=
mean