In[]:=
(*deployswithcanonicalname*)deploy:=Module[{notebookFn,parentDir,cloudFn,result},Print[DateString[]];notebookFn=FileNameSplit[NotebookFileName[]][[-1]];parentDir=FileNameSplit[NotebookFileName[]][[-2]];cloudFn=parentDir~StringJoin~"/"~StringJoin~notebookFn;result=CloudDeploy[SelectedNotebook[],CloudObject[cloudFn],Permissions"Public",SourceLinkNone];Print["Uploading to ",cloudFn];result];deploy
Mon 12 Sep 2022 17:46:50
In[]:=
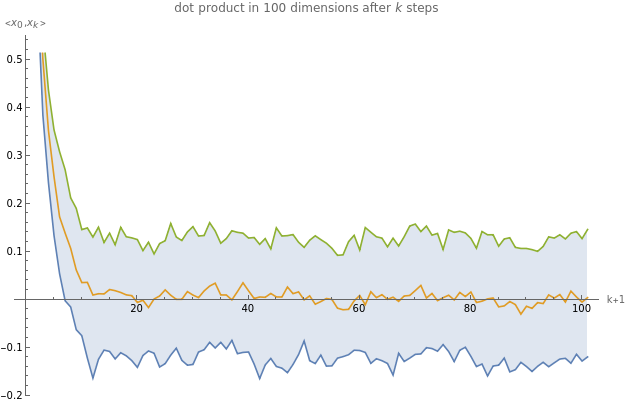
b=100;d=100;cos[vec1_,vec2_]:=;batchCos[batch1_,batch2_]:=MapThread[cos[#1,#2]&,{batch1,batch2}];x0=A0=Table[{1}~Join~ConstantArray[0,d-1],b];normalize[batch_]:=Normalize/@batch;step[batch_]:=normalizebatch+RandomVariate[NormalDistribution[],{b,d}],>"},PlotLabel->StringForm["dot product in `` dimensions after `` steps",d,k],Filling->{1->{3}}]
vec1.vec2
Norm[vec1]Norm[vec2]
d
;vals=NestList[step,x0,100];stats[batch_]:={Quantile[batch,.1],Quantile[batch,.50],Quantile[batch,.9]};ListLinePlot[(stats[batchCos[x0,#]]&/@vals),AxesLabel->{"k+1","<x
0
x
k
Out[]=
Is second step in the “away” direction or orthogonal?
Is second step in the “away” direction or orthogonal?
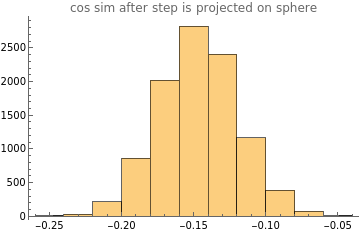
TLDR steps don’t occur at orthogonal angles but slightly anti-correlated. Probably due to sphere normalization
In[]:=
b=10000;d=1000;z:=RandomVariate[NormalDistribution[],{b,d}];batchCos[{batch1_,batch2_}]:=MapThread[cos[#1,#2]&,{batch1,batch2}];normalize[batch_]:=Normalize/@batch;v1=Table[{1}~Join~ConstantArray[0,d-1],b]//normalize;v1=normalize[z];v2=normalize[v1+z];v3=normalize[v2+z];vals=batchCos[{v2-v1,v3-v2}];Histogram[vals,PlotLabel->"cos sim after step is projected on sphere"]Median[vals]
d
;cos[vec1_,vec2_]:=vec1.vec2
Norm[vec1]Norm[vec2]
Out[]=
Out[]=
-0.146763