In[]:=
deploy
Mon 5 Jul 2021 16:00:07
Normalize so that f(n,0)=1
Normalize so that f(n,0)=1
In[]:=
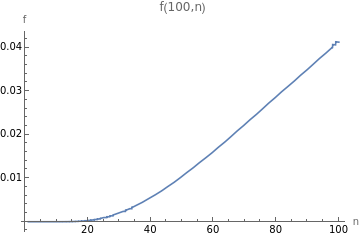
f[s_,n_]:=Sum,{i,1,n};Plot[f[100,n],{n,1,100},PlotLabel"f(100,n)",AxesLabel{"n","f"}]
1
HarmonicNumber[n]
s
1-
1
i
1
i
Out[]=
In[]:=
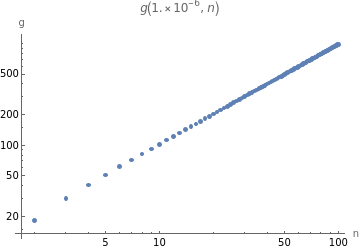
eps=;ClearAll[ff];doit[n_,x0_]:=s/.FindRoot[f[s,n]eps,{s,x0},WorkingPrecisionLog[2,n]+$MachinePrecision];ff[1]=1;ff[n_Integer]:=ff[n]=doit[n,ff[n-1]];data=Table[{n,ff[n]},{n,2,100}];ListLogLogPlot[data,PlotLabelg[N@eps,n],AxesLabel{"n","g"}]
-6
10
Out[]=
Katsurda result check
Katsurda result check
original formula
original formula
In[]:=
katsurda[x_]:=NSumZeta[j],{j,2,Infinity};katsurdaApprox[x_]:=x(Log[x]+2EulerGamma-1)-Zeta[0];
j
(-x)
j!
In[]:=
plot1=Plot[katsurda[x],{x,0,30}];plot2=DiscretePlot[katsurdaApprox[x],{x,0,30,2}];Show[plot1,plot2]
Out[]=
derivative formula
derivative formula
In[]:=
dkatsurda[x_]:=NSumZeta[j+1],{j,1,Infinity};dkatsurdaApprox[x_]:=Log[x]+2EulerGamma;plot1=Plot[dkatsurda[x],{x,0,30}];plot2=DiscretePlot[dkatsurdaApprox[x],{x,0,30,2}];Show[plot1,plot2]
-
j
(-x)
j!
Out[]=