In[]:=
Thu 21 Dec 2023 11:00:12
From “linear-estimation.nb: Get Choi representation ...” and linear-estimation-scratch-nov: Choi
Connecting Choi matrix of T to contraction properties of T
Connecting Choi matrix of T to contraction properties of T
Util
Util
Main example
Main example
In[]:=
Clear[EE,covStep,choi];X={{1,0},{1,1}};(*X=X/Norm[X,"Frobenius"];*)b=1;d=Length[First@X];ii=IdentityMatrix[d];batches=Subsets[X,{b}];(*Unfoldedoperatorview*)EX2=Mean[#.#&/@batches];EX4=Mean[(#.#)⊗(#.#)&/@batches];Tflat=ii⊗ii-ii⊗EX2-EX2⊗ii+EX4;Tflat≐Mean[(ii-#.#)⊗(ii-#.#)&/@batches];(*Choimatrixgivesoperatorinnaturalbasis*)EE[i_,j_]:=Array[Boole[#1i&j]&,{d,d}];covStep[cov_]:=Mean[(ii-#.#).cov.(ii-#.#)&/@batches];choi=ArrayFlatten@Table[covStep@EE[i,j],{i,1,d},{j,1,d}];unvecMap=Map[unvec[#]&,Partition[Tflat,d],{2}];fl1[l_]:=Flatten[l,{1}];vec2[mat_]:=Join@@Transpose@mat;coords=fl1@Outer[List,Range[d],Range[d]];{"T rearrangement=choi: ",ArrayFlatten[unvecMap]≐choi}{"T vectorized arrangement: ",Tflat≐(vec2[covStep[EE@@#]]&/@vec2@coords)}SeedRandom[1];A=RandomReal[{-1,1},{d,d}];A=A.A;{"Choi construction: ",choi≐choiFromTflat[Tflat]}kraus1=unvec/@symsqrtFactors[choi];kraus=getKraus@Tflat;kraus≐kraus1;osrApply[A_]:=Total[#.A.#&/@kraus];{"Kraus=covStep: ",osrApply[A]≐covStep[A]}t[stuff_]:=StringForm["``",stuff];TableForm[{{"Ai",t[MatrixForm[(ii-#.#)]&/@batches]},{"Kraus",t[MatrixForm/@getKraus[Tflat]]},{"Choi",choi//MatrixForm},{"Choi evals",t@Eigenvalues[choi]},{"T",Tflat//MatrixForm},{"T evals",t@Eigenvalues[Tflat]}}]
2
n
Linearly dependent example
Linearly dependent example
Adding 0 observation makes Choi and T matrix have identical eigenvalues up to sign
Out[]//TableForm=
Ai |
| ||||||||||||||||
Kraus |
| ||||||||||||||||
Choi |
| ||||||||||||||||
Choi evals | 2 3 1 3 1 3 | ||||||||||||||||
T |
| ||||||||||||||||
T evals | 2 3 1 3 1 3 |
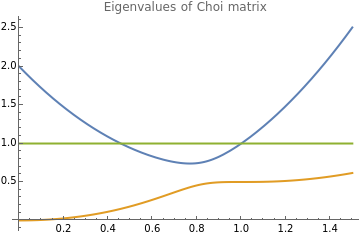
T vs M eigenvalues
T vs M eigenvalues
M eigenvalues close to 1 suggest preservation of quantum states
T eigenvalues can be negative.
Eigenvalues of M close to 1 suggest Fidelity is preserved (effective rank not dropping?)
T eigenvalues can be negative.
Eigenvalues of M close to 1 suggest Fidelity is preserved (effective rank not dropping?)
Out[]=
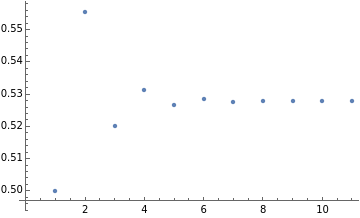
Growth of purity
Growth of purity
Out[]=